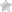Как определить режим движения жидкости в трубе

Цель работы: Изучение изменений, проходящих в потоке при различных режимах течения.

Теоретическая часть

Большинство процессов химической технологии связаны с движением газа или жидкости, причем характер этого движения существенно сказывается на ходе процесса. При расчете таких процессов необходимо учитывать характер движения потоков, жидкости или газа.

Исследуя течение капельных жидкостей в трубах, английский ученый Рейнольдс (1883 г.) обнаружил существование двух различных режимов ее течения.

Обычно при малых скоростях и малых диаметрах трубопровода, элементарные струйки жидкости движутся параллельно, как бы скользя друг по другу, не перемешиваясь. Такое течение называют вязким или ламинарным. Распределение скоростей поперечному сочетанию трубопровода при ламинарном течении происходит по параболе, причем средняя скорость потока составляет 0,5 от максимальной

wср= 0,5 w max (2.1)

При больших скоростях наблюдается поперечное перемешивание струек жидкости за счет образованных вихрей и движение частиц жидкости хаотическое, этот вид течения называется турбулентным. При таких скоростях характер течения различен поперечному сечению потока.

У стенки течет тонкий ламинарный слой толщиной d. В центральной части потока находится сфера вихревого движения с радикальным перемешиванием. Ламинарный слой отделяется от вихревого так называемым буферным слоем.

Распределение скоростей при этом режиме пологой кривой и средняя скорость потока составляет 0,8 — 0,9 от максимальной.

wср = (0,8 ¸ 0,9) wmax (2.2)

Характер движения жидкости (газа) зависит, как показали опыты, не только от скорости потока, но и от геометрических размеров потока, вязкости и плотности жидкости (газа). Влияние перечисленных физических параметров потока на характер движения определяется величиной безразмерного комплекса- критерия, названного в честь ученого, открывшего это явление, числом Рейнольдса:

где: w–средняя скорость потока, м/с;

dэ–эквивалентный диаметр трубопровода, м;

• r–плотность жидкости (газа), кг/ м3;
• —динамический коэффициент вязкости, Па . с;
• n = — кинематический коэффициент вязкости, м2/с.

Число Рейнольдса показывает соотношение сил инерции, характеризующихся скоростью потока и его размерами, и сил внутреннего трения, характеризующихся вязкостью потока.

Отсюда следует, что турбулентное течение свойственно потокам, обладающим развитыми силами инерции, а ламинарное течение характерно для потоков, в которых силы внутреннего течения преобладает над силами инерции.

Установлено, что для ламинарного режима численное значение числа Рейнольдса всегда меньше некоторого определенного «критического» значения, для прямых труб критическое значение Reкр = 2300.

Необходимо отметить, что приведенное критическое значение является в известной степени условным, так как трудно обнаружить резкий переход от ламинарного режима к турбулентному.

В действительности обычно наблюдается так называемая «переходная» область исчезновения ламинарного режима и установления турбулентного состояния потока.

Численные значения числа Рейнольдса для потоков, проходящих по прямым трубам, характерны следующие значения числа Рейнольдса:

1. Ламинарное течение — Re < 2300
2. Переходная область — 2300 £ Re £ 10000
3. Развитое турбулентное течение — Re ³ 10000

Для потоков, проходящих по изогнутым трубам (змеевикам), критическое значение Reкр выше, чем в прямых трубах, и зависит от отношения диаметра трубы dзмеевика к диаметруD витков змеевика (d /D)/1, стр. 18/.

При движении жидкости через сечение любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Под гидравлическим радиусом rг понимают отношение площади затопленного сечения потока к смоченному периметру:

• Для круглой трубы с внутренним диаметром d и, значит, площадью свободного сечения S = πd2 / 4 при сплошном заполнении его жидкостью П = π d, откуда гидравлический радиус:
• rr = (2.4 а)
• Следовательно, для потоков некруглого сечения вместо диаметра можно применить эквивалентный диаметр:
• d э = = 4ru = d (2.5)
• Для круглой трубы: dэ = dвн.
• Для канала прямоугольного сечения со сторонами полностью заполненного жидкостью, гидравлический радиус:
• rг= 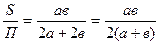(2.6)
• а эквивалентный диаметр:
• d э = 4rг = rг = 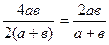( 2.6а)
• Описание установки

Схема установки приведена на рис 2.1. Воду из городского водопровода подают в бак 1 по трубе 3, регулируя подачу вентилем 4. Для предупреждения переполнения бака установлена переливная труба 5. Для слива воды из бака установлена воронка 6 на трубе (линия канализации).

Во время работы установки вода из бака 1 по питательной трубе 10 через вентиль 11 поступает в расходный бак 12. Излишек воды через трубу сливается в канализацию.

Из расходного бака 12 вода по стеклянной трубе 14 поступает в буферный бак 15 и сливается из него через регулировочный вентиль 16 и ротаметр 12 в канализацию.

Из бака с краской 18 через кран 19 по тонкой трубе 20 подкрашенная струйка воды поступает в стеклянную трубу 14.

По окончании работы для опорожнения баков 15 и 12 пользуется соответственно вентилями 21 и 22.

Для успешного проведения опытов весьма важными условиями являются стабилизация потока в стеклянной трубе 14 и согласование скоростей истечения краски со скоростью самого потока. В этих целях приняты следующие меры.

Так как в городском водопроводе наблюдается временами колебания напора и пульсаций потока, то воду из водопровода подают сначала в запасный бак 1 достаточно большой вместимости. Затем вода поступает в расходный бак 12 по питательный трубе 10. Постоянный уровень воды в баке 12 поддерживается с помощью переливной трубы 13.

Для согласования скорости истечения краски со скоростью воды в стеклянной трубе 14 бак с краской 18 закреплен на наружной высоте для создания необходимого напора при истечении краски. Расход краски регулируется краном 19.

Методика проведения работы

Работу начинают с установления ламинарного режима и, увеличивая постепенно скорость движения воды в стеклянной трубе, наблюдают за изменениями, происходящими с подкрашенной струйкой при разных режимах течения.

Перед началом работы проверяют наличие воды в баке 1 по водомерному стеклу 2. Если вода в баке меньше половины, то открывают вентиль 4 и заполняют бак, следя за уровнем воды в водомерном стекле 2. Затем заполняют баки 10 и 15, открывая вентиль 11. Затем понемногу открывают вентиль 16, устанавливая по ротаметру 17 минимальный расход воды.

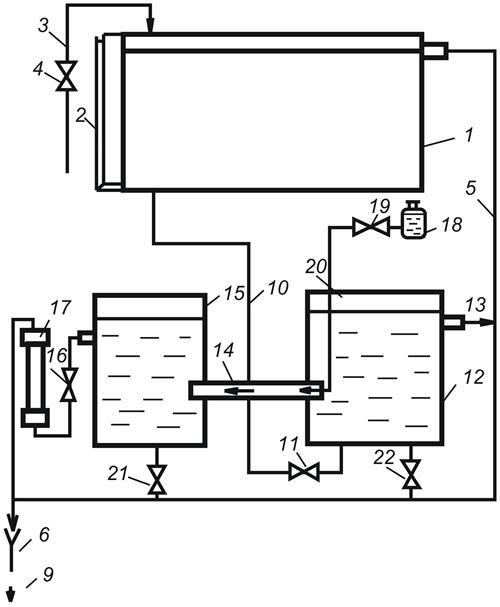
Рис.2.1. Схема экспериментальной установки.

В первой части работы для пуска подкрашенной струйки постепенно открывают кран 19, регулируя степень открытия вентилей 11 и 16 и крана 1, Добиваются четкого очертания подкрашенной струйки, хорошо видимой на освещенном фоне – экрана.

Затем, увеличивая степень открытия вентиля 15, повышают тем самым скорость воды в стеклянной трубе 14, вследствие чего ламинарный режим начинает нарушаться и переходить в турбулентный.

При этом надо регулировать открытие крана 19, а также вентиля 11, не позволяя уровню воды в баке 12 опускаться ниже переливной трубы 13.

Во второй части работы производят замеры, необходимые для определения значения число Рейнольдса при разных режимах течения, Настраивают установку на ламинарный режим и приступают к определению расхода по ротаметру 17. Таких замеров проводят несколько раз (6-7), заканчивая их при развитом турбулентном движения.

1. Обработка опытных данных
2. Определить скорость движения воды в стеклянной трубе, через массовый расход воды:
3. w =
4. где: G — массовый расход воды, кг/ с;
5. r — плотность воды, кг/м3
6. d BH – внутренний диаметр стеклянной трубы (d = 20 мм), м.
7. Массовый расход воды определяется из уравнения расхода:
8. G = V r
9. где: V – объемный расход воды, м3/сек.
10. Вычисляют число Re и определяют режим течения:
11. где: ν – кинематический коэффицент вязкости.

Определить число Рейнольдса для случаев прохождения жидкости через прямоугольное и квадратное сечения трубопроводов со сторонами «a» и «b». Значения сторон выдается преподавателем каждому студенту. При этом для определения скорости воды можно использовать экспериментальные значения расхода воды.

Результаты наблюдаемые, опытные и расчетные данные заносят в отчетную таблицу.

Таблица 2.1. Протокол наблюдений

№ п/п

Расход воды G, кг/с

Температура воды, tу , 0С

Скорость движения воды w, м/с

Число Рейнольдса Re

Состояние подкрашенной струйки

Режим потока

2.5. Контрольные вопросы

1. Какое течение называется ламинарным?

2. Как определить среднюю скорость потока движущегося ламинарно?

3. Какое течение называется турбулентным?

4. Какого соотношение между средней и максимальной скоростями потока при турбулентном течении?

5. Что такое эквивалентный диаметр и гидравлический радиус?

6. Что такое число Рейнольдса? Каков его физический смысл?

7. В каком интервале числе Рейнольдса наблюдают «переходную» область?

8. От каких параметров зависит значение Re для змеевиков?

ЛАБОРАТОРНАЯ РАБОТА № 3

Основы гидравлики



Почему так происходит, и в какой момент в спокойном и ласковом потоке вдруг просыпается безумный бурлящий «демон»? Можно ли предсказать поведение потока в тех или иных условиях? Давайте попробуем разобраться в этом вопросе с точки зрения современной науки.

• Рассмотрим потоки, характеризуемые условием неразрывности – в любой момент времени расход жидкости постоянен во всех сечениях, т. е соблюдается соотношение:
• v1S1 = v2S2 = v3S3 = … = vS,
• где v1, v2, v3,…v – соответственно средние скорости потока в разных сечениях.
• Наблюдения за такими потоками показывают, что в природе существуют два различных вида движения жидкости: во-первых, слоистое, упорядочное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и, во-вторых, неупорядоченное, так называемое турбулентное движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание частиц и слоев.
• Иногда выделяют третий режим движения жидкостей — переходный, при котором упорядоченное движение частиц очень неустойчиво, и при малейшем изменении условий перемещения потока может произойти переход от ламинарного режима к турбулентному, и наоборот.
• ***

Число Рейнольдса

Наблюдательными людьми давно подмечено, что вязкие жидкости (например, масла) движутся большей части упорядоченно, а маловязкие жидкости (вода, бензин, газообразные вещества) — почти всегда неупорядоченно.

Кроме того, на характер движения жидкости явно влияет скорость потока — медленно перемещающаяся по руслу жидкость ведет себя спокойно, но стоит увеличить ее скорость, и картина может измениться.

Однако установить математическую зависимость между характером движения потока и его параметрами долгое время не удавалось никому.

Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 году в результате опытов английского физика О. Рейнольдса.

О. Рейнольдс определил общие условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому.

Оказалось, что состояние (режим) потока жидкости в трубе зависит от величины некоторого безразмерного числа, учитывающего основные факторы, определяющие это движение: среднюю скорость, диаметр трубы (или другие линейные характеристики потока), плотность жидкости и ее вязкость.

1. Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:
2. Re = ρvR/µ,
3. где: R – гидравлический радиус потока; v – скорость потока; µ — динамическая вязкость жидкости, ρ – плотность жидкости.
4. Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной.

Осборн Рейнольдс (Osborne Reynolds, 1842-1912) — английский механик, физик и инженер, специалист в области гидромеханики и гидравлики. Член Лондонского королевского общества с 1877 г. В 1883 г. он установил общий принцип прогнозирования режима движения жидкости при помощи упомянутого выше числа.

Выводами и умозаключениями Рейнольдса потомки пользуются и в наши дни при гидравлических расчетах.

Тем не менее, несмотря на то, что вопрос о неустойчивости ламинарного движения и его переходе в турбулентное, а также о величине критического числа Рейнольдса долгое время является предметом тщательных теоретических и опытно-экспериментальных исследований, до сих пор его полного решения так и не получено.

Поскольку динамическая вязкость жидкости связана с кинематической вязкостью соотношением µ = ρν, то критерий Рейнольдса можно записать в виде:

Re = vR/ν    (1).

Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер. Эти границы характеризуются критическими значениями числа Рейнольдса: нижним Reкр и верхним Re'кр.

При Re < Reкр наблюдается устойчивый ламинарный режим течения жидкости, при Re > Re'кр – устойчивый турбулентный режим, а в интервале чисел Рейнольдса Re'кр> Re > Reкр режим течения жидкостей неустойчивый, т. е.

ламинарный режим может легко переходить в турбулентный.

• Формулу (1) применяют при определении числа Рейнольдса для потока любого сечения. Для круглых цилиндрических труб с внутренним диаметром d:
• Red = vd/ν.
• Поскольку для таких труб гидравлический радиус R = 4d, то
• Re = 4Red = 4vd/ν.

При проведении гидравлических расчетов цилиндрических труб обычно принимают Re = 250…500, Re'кр = 575. При этом Red будет равен: Redкр = 1000…2000, Red'кр = 2300.

Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах увеличивается.

По критическому значению числа Рейнольдса легко можно определить также критическую скорость, т. е. скорость, ниже которой будет иметь место ламинарное движение жидкости:

1. vкр = Reкрv/d = 2300v/d.
2. Ламинарному и турбулентному режимам движения жидкости соответствует и различное распределение скоростей частиц по живому сечению потока.
3. ***



При ламинарном режиме течения жидкости по трубе (см. рис. 1) максимальная скорость наблюдается у частиц жидкости, движущихся по центральной оси трубы, а минимальная – у стенок трубы. Частицы подвижной жидкости, расположенные у стенок трубы буквально «прилипают» к стенкам благодаря силам трения и практически неподвижны.

По мере удаления от стенок трубы скорость частиц жидкости возрастает, поскольку на их движение влияет лишь трение между отдельными слоями (элементарными струйками) жидкости. Исследования показали, что при ламинарном режиме движения жидкости изменение скорости в поперечном сечении потока происходит по параболическому закону, т. е.

эпюру скоростей частиц можно представить в виде параболы (см. рис. 1).

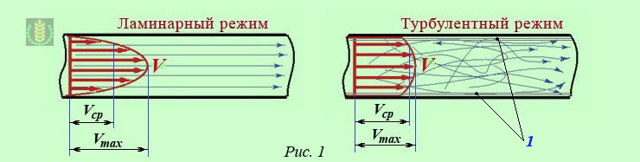
При турбулентном режиме течения жидкости распределение скоростей более равномерное по сечению потока, чем при ламинарном режиме. Это связано с перемешиванием частиц жидкости, имеющих разную скорость в слоях, и относительным выравниванием средней скорости на всей площади сечения потока. Т. е.

отдельные частицы турбулентного потока могут иметь в одном и том же сечении весьма различные по величине и направлению скорости, однако эпюра (график) средней скорости всех частиц по сечению будет ровнее, чем при ламинарном режиме движения. Лишь слои жидкости, прилегающие к стенкам трубы (поз.

1 на рисунке), движутся с малой скоростью, и режим движения здесь наблюдается ламинарный, несмотря на то, что весь поток характеризуется турбулентным режимом движения.

По этой причине можно утверждать, что «чистого турбулентного режима» движения жидкости не существует, поскольку граничные со стенками слои жидкости в любом случае имеют ламинарный характер движения.

Однако толщина ламинарного слоя несравненно мала в сравнении с сечением потока, в котором частицы жидкости перемещаются хаотично (турбулентно), поэтому такой режим течения жидкости принято считать турбулентным.

***

Пример решения задачи с использованием числа Рейнольдса

Определить режим движения нефти в трубопроводе диаметром d = 400 мм при скорости движения v = 0,13 м/с. Кинематическая вязкость нефти ν = 0,3×10-4 м2/с.

• Решение:
• Определим число Рейнольдса для данного режима движения жидкости (нефти):
• Red = vd/ν = 0,13×0,4/0,3×10-4 = 1733.

Для круглых труб критические значения числа Рейнольдса имеют величину: Redкр = 1000…2000, Re'dкр = 2300. Сравнив полученное расчетное значение с критическими значениями числа Рейнольдса, делаем вывод, что Red < Redкр, т. е. движение нефти в трубопроводе будет ламинарным.

1. Другие задачи на использование числа Рейнольдса для определения режимов движения жидкостей представлены здесь.
2. ***
3. Уравнение Бернулли



Главная страница

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71

Специальности

Учебные дисциплины

Олимпиады и тесты

Режимы течения жидкости в трубах

Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный.

Указанные течения жидкости можно наблюдать на приборе, представленном на рисунке 3.11. Он состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С па конце, и сосуда D с индикаторной подкрашенной жидкостью, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.

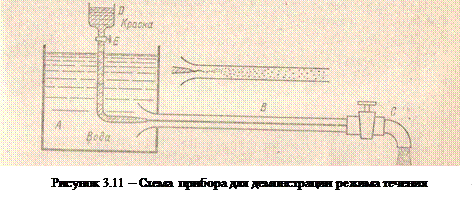Если несколько приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить индикаторную жидкость в поток воды, то увидим, что введенная в трубу подкрашенная жидкость не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Пьезометр или трубка Пито, присоединенные к трубе, покажут неизменность давления и скорости по времени, отсутствие колебаний (пульсаций). Это так называемое ламинарное (слоистое) течение.

При постепенном увеличении скорости течения воды в трубе путем открытии крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение.

Струйка подкрашенной жидкости по выходе из трубки начинает колебаться, затем размываться и перемешиваться с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости.

Пьезометр и трубка Пито показывают непрерывные пульсации давления и скоростей в потоке воды. Течение становится, как его принято называть, турбулентным (см. рисунок3.11, вверху).

Если уменьшить скорость потока, то восстановится ламинарное течение.

Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т. е. прямолинейно; отсутствуют поперечные перемещения жидкости.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений.

При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости.

Режим течения данной жидкости в данной трубе изменяется при вполне определенной средней по сечению скорости течения υ кр, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости v и обратно пропорционально диаметру d трубы, т. с.

• Входящий в эту формулу безразмерный коэффициент пропорциональности k одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью v:
• k = υкр d/v.
• Полученное безразмерное число называется критическим числом Рейнольдса и обозначается

Reкр = υкр d/v. (3.19)

1. Критическое число Рейнольдса Reкр не зависит от рода жидкости и размеров сечения, а лишь в небольшой степени определяется формой сечения и шероховатостью стенок трубы.
2. Таким образом, критическое число Рейнольдса является критерием, определяющим режим течения в трубах.
3. Как показывают опыты, для труб круглого сечения Reкр ≈ 2300.
4. Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с Reкр , определить режим течения жидкости.
5. При Re < Reкр течение является ламинарным, при Re > Reкр — турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при

Re ≥ 10000, а при Re = 2300 … 10000 имеет место переходная, критическая область.

На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты и другие маловязкие жидкости.

Новая страница 1

• Лабораторная работа №3. Определение режима движения жидкости
• Цель работы:
• Наблюдение за различными режимами движения жидкости в трубе и определение числа Рейнольдса.
• 1. Теоретические сведения

При течении жидкости возможны два режима движения: ламинарный и турбулентный.

Наличие того или иного режима определяется соотношением сил, действующих в движущейся жидкости, а именно, сил инерции и сил внутреннего трения (вязкости). Если в потоке преобладают силы внутреннего трения, то устанавливается ламинарный режим.

Отношение сил инерции к силам внутреннего трения характеризуется так называемым критерием режима движения (число Рейнольдса), который для напорного движения определяется соотношением

(1)

1. где d — внутренний диаметр трубы, м;
2. V — средняя скорость движения жидкости в потоке, м/с; ν — кинематический коэффициент вязкости жидкости, м2/с.
3. Каждому режиму движения соответствует определенная область значений числа Рейнольдса, не зависящая от свойств жидкости.
4. Смена режима (переход ламинарного режима в турбулентный или, наоборот, турбулентного в ламинарный) связана с критической величиной этого числа, обозначаемой Reкр.

Для напорного движения в трубах нижнее критическое число Рейнольдса, соответствующее переходу турбулентного режима в ламинарный, следует считать равным 2300.

Верхнее критическое число Рейнольдса, соответствующее переходу ламинарного режима в турбулентный, не является столь определенным, как нижнее, численное значение его можно принять приблизительно равным 4000.

В интервале чисел Рейнольдса от 2300 до4000 возможно существование того или другого режимов.

Скорость движения жидкости, при которой происходит смена режимов, называется критической скоростью. В отличие от критического значения числа Рейнольдса, одинакового для потока любой жидкости в трубопроводе любого диаметра, критическая скорость для каждой жидкости имеет свое определенное значение, зависящее от диаметра трубопровода и коэффициента вязкости жидкости.

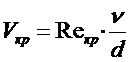(2)

Характер движения частиц при ламинарном и турбулентном режимах различен. При ламинарном режиме частицы перемещаются как бы слоями по траекториям, параллельным между собой. При турбулентном режиме траектория движения частиц криволинейна и сложна. Частицы при движении сталкиваются между собой, и происходит довольно интенсивный процесс перемещения.

Движение частиц можно сделать видимым, окрасив поток.

Таким образом, установить режим движения можно двумя методами: определением числа Рейнольдса и визуальным методом, наблюдая за движением частиц в подкрашенном потоке.

ЕЕсли краска, добавленная к потоку, располагается в нем в виде прямой струйки, отчетливо видной на всем протяжении, это свидетельствует о параллельном перемещении частиц жидкости, или о наличии ламинарного режима движения. При этом число Рейнольдса оказывается меньше критического значения, т. е. меньше 2300.

Если струйка краски размывается потоком и равномерно окрашивает его, это свидетельствует о движении частиц по сложным траекториям, что приводит к перемешиванию, или о наличии турбулентного режима. При этом число Рейнольдса — больше критического, т. е. больше 2300.

2. Проведение работы

Лабораторная работа по определению режима движения производится на установке, схематически изображенной на рис. 1.

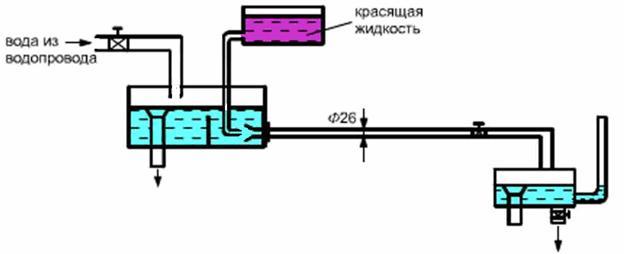
Рис. 1. Схема лабораторной установки.

Водопроводная вода поступает в напорный бак с некоторым избытком и протекает в стеклянную трубу внутренним диаметром 26 мм, а затем в приемный бак, откуда уходит в канализацию. В напорном баке установлена переливная воронка и успокаивающая перегородка. Над напорным баком расположен сосуд, из которого краска по тонкой трубке поступает в стеклянную трубку.

Исследование характера движения проводится при равномерном движении. Как известно, равномерным движением жидкости называют установившееся движение в трубопроводе, по длине которого средняя скорость движения остается постоянной.

Установившееся движение жидкости возможно в условиях постоянного напора и неизменных гидравлических сопротивлений системы. В этом случае объемный расход жидкости остается постоянным по времени.

Постоянство напора в установке обеспечивается неизменным положением свободной поверхности в напорном баке, совпадающим с верхней кромкой переливной воронки. Напор в данном случае определяется вертикальным расстоянием от верхней кромки переливной воронки до выходного сечения трубопровода.

Постоянство гидравлического сопротивления достигается неизменной степенью открытия во время опыта вентиля на конце трубопровода.

Для начала работы необходимо установку наполнить водой и создать движение жидкости в трубопроводе, что осуществляется некоторой степенью открытия запорного крана.

Изменение скорости движения в стеклянной трубке достигается различной степенью открытия вентиля.

Установив малую степень открытия крана (при большом сопротивлении), получаем малую скорость движения. Одновременно с визуальным наблюдением за потоком определяется критерий режима движения или число Рейнольдса.

Для определения числа Рейнольдса необходимо измерить внутренний диаметр стеклянной трубки и вычислить среднюю скорость потока. Среднюю скорость жидкости находят из уравнения неразрывности потока.

Для этого необходимо определить расход жидкости, например, объемным методом:

• где V — объем, набранной в мерный сосуд, жидкости, мЗ; τ — время, с.
• Откуда:
• где Q — объемный расход, или объем жидкости, протекающей через площадь живого сечения в единицу времени, мЗ/с;

S — живое сечение потока, т.е. сечение, расположенное нормально к направлению движения, м2;

V — средняя скорость движения жидкости, м/с.

Если в начале опыта установлен ламинарный режим, то дальнейшие испытания проводят, увеличивая скорость движения (уменьшая сопротивление) до критического ее значения и далее до сверхкритического, при котором существует турбулентный режим движения.

Число Рейнольдса определяют по уравнению (1). Кинематический коэффициент вязкости жидкости определяют по табл. 1 в зависимости от t. жидкости. Значение критической скорости находят по уравнению (2).

Результаты испытаний и окончательные расчеты сводят в табл. 2.

Таблица 1.   Кинематический коэффициент вязкости жидкости

t, °C	0	5	10	15	20	30	40	50
ν см2/с	0,0178	0.0152	0,0131	0.0114	0,0101	0.0081	0,0066	0,0055

Таблица 2

Номер опыта	Результаты наблюдений	Вычисленные величины
Режим	d, м	V, м3	τ, с	t, °С	S, м2	Q, м3/с	V, м/с	ν. м2/с	Re	Vкр, м/с
1
2
3
4
5

3. Порядок выполнения виртуальной лабораторной работы

Кнопкой «Пуск воды» запустите процесс заполнения напорного бака и прозрачной горизонтальной трубы водой. После наполнения напорного бака до верхнего уровня переливной воронки, приступайте к открыванию главного вентиля. Управлять вентилем можно, как непосредственно одиночными щелчками левой кнопкой мыши, так и клавишей со стрелкой «вправо».

Управляя степенью открытия вентиля, Вы сможете только увеличивать скорость протекания воды. Уменьшать поток в этой лабораторной работе нельзя по техническим причинам демонстрационного ролика.

Если понадобится вернуться к меньшей скорости течения воды, придётся воспользоваться кнопкой «сброс», повторить процесс наполнения бака водой и снова установить нужную скорость.

Для визуализации режима течения в трубе необходимо открыть вентиль, перекрывающий красящую жидкость, для чего достаточно кликнуть по нему левой кнопкой мыши. Этот вентиль откроется только в том случае, если главный вентиль будет открыт хотя бы на одно деление.

Открыв вентиль красящей жидкости, можно будет наблюдать режим движения жидкости в прозрачной горизонтальной трубе. В зависимости от степени открытия главного вентиля, можно будет наблюдать вначале ламинарный поток жидкости, постепенно переходящий в турбулентный.

При этом, ламинарным режимом нужно считать только тот, при котором струя красящей жидкости в общем потоке абсолютно не искажается, а турбулентным — тот, при котором струя краски полностью размывается.

Для измерения скорости потока достаточно кликнуть левой кнопкой мыши по спускному клапану, после чего опорожнится мерный сосуд и автоматически запустится таймер.

Как только в мерном сосуде наберётся достаточное количество воды, остановите таймер и занесите в таблицу 2 измеренный объём воды V и время таймера  .

Кроме того в таблицу необходимо также внести температуру воды t и диаметр d прозрачной горизонтальной трубы.

Измерения повторяют как минимум для двух режимов — ламинарного и турбулентного.

Далее переходите к вычислениям и заполните необходимые ячейки таблицы 2. Сделайте выводы по работе.

4. Контрольные вопросы

1. Назовите режимы движения жидкости и укажите их характерные особенности.

2. Поясните, что такое критерий Рейнольдса, и назовите факторы, от которых он зависит.

3. Поясните, что такое критическое число Рейнольдса?

4. Поясните, каким образом при гидравлических расчётах определяют режим движения жидкости и, с какой целью?

5. Поясните, что такое критическая скорость, от каких факторов она зависит и как её определяют?

Справка по числу Рейнольдса. Калькулятор числа Рейнольдса. Виды режимов движения сред

Число Рейнольдса —
безразмерная величина, характеризующая отношение инерционных сил к силам вязкого трения в вязких жидкостях и газах.

Число Рейнольдса также является критерием подобия течения вязкой жидкости.

Общие сведения

Число Рейнольдса обозначается в физике и инженерных расчетах — Re. Широко применяется при гидравлических и аэродинамических расчетах различных систем.

Число Рейнольдса служит для определения (является критериям) режима движения среды (жидкости или газа) в системе.

Различают несколько режимов движения жидкостей и газа:

• • ламинарный;
  • смешанный (иногда встречается, как критический);
  • турбулентный.

Критерием перехода из одного режима в другой служит критическое значения числа Рейнольдса — Reкр. В расчетах обычно считается, что при ReReкр возможно возникновение турбулентности. Смешанный режим обычно относят к турбулентному режиму, как неустойчивая турбулентность.

Для систем трубопроводов с круглыми трубами с очень гладкими стенками критическое значения числа Рейнольдса обычно принимается  Reкр≈ 2100÷2300.

Критическое значения числа Рейнольдса зависит от:

• • от конкретного вида течения (например от формы сечения канала, обтекания шара и т. п.);
  • различных возмущений потока (вызывающих изменение направления и модуля вектора скорости потока, например любые местные сопротивления, шероховатости стенок и т.п.).

На основании числа Рейнольдса и исходя из режима движения жидкости или газа при гидравлическом и аэродинамическом расчете определяется коэффициент гидравлических потерь λ (коэффициент путевых потерь).

Существуют методики расчета числа Рейнольдса, учитывающие в себе все выше указанным зависимости. Например расчет числа Рейнольдса при гидравлическом расчете газопроводов согласно методике СП 42-101-2003, разбивает турбулентный режим движения газа на несколько под режимов учитывающих:

• • режим движения газа (включая смешанный/критический);
  • шероховатость стенки трубы.

Формулы расчет числа Рейнольдса. Калькуляторы числа Рейнольдса онлайн

Классическая формула расчета числа Рейнольдса

Re=(u*D)/υ,

где u — характерная скорость, м/с; D — гидравлический диаметр, м; υ — кинематическая вязкость среды, м2/с.

Скачать результат расчета числа Рейнольдса: Поделится ссылкой на расчет :

Формула расчета числа Рейнольдса через плотность

Re=(ρ*u*D)/η,

где ρ — плотность среды, кг/м3; u — характерная скорость, м/с; D — гидравлический диаметр, м; η — динамическая вязкость среды, Па·с или кг/(м·с).

Скачать результат расчета числа Рейнольдса: Поделится ссылкой на расчет :

Формула расчета числа Рейнольдса через объемный расход жидкости или газа

Re=(Q*D)/(υ*S),

где Q— объёмный расход потока, м3/с; D — гидравлический диаметр, м; υ — кинематическая вязкость среды, м2/с; S — площадь сечения канала (например: трубы, воздуховода и т.п), м2.

Скачать результат расчета числа Рейнольдса: Поделится ссылкой на расчет :

Формула расчета числа Рейнольдса природного газа согласно методике СП 42-101-2003 (п.3.28)

Re=(0.0354*Q)/(d*υ),

где Q— объёмный расход газа при нормальных условиях, м3/ч; d — внутренний диаметр газопровода, см; υ — кинематическая вязкость среды, м2/с.

Скачать результат расчета числа Рейнольдса в газопроводе: Поделится ссылкой на расчет :

Видеоматериал по теме «Число Рейнольдса»

Поделиться ссылкой: