- №1
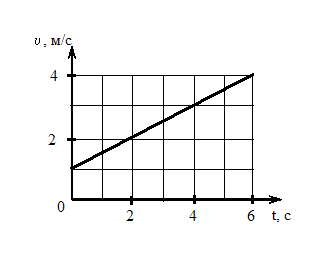На рисунке приведен график зависимости скорости тела v от времени t. Если масса тела равна 2 кг, то сила (в Н), действующая на тело, равна … - Решение: Из второго закона Ньютона F=ma, где а – модуль ускорения, который можно найти из графика зависимости v(t):
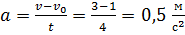. Тогда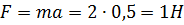 
- №2 На рисунке приведен график зависимости скорости тела v от времени t. Если масса тела 1,5 кг, то изменение импульса тела (в единицах СИ) за первые 4 с движения равно …
- Ответ: 3
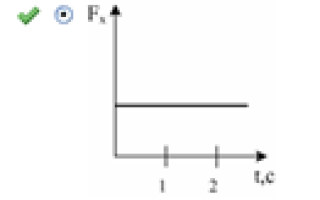
№3Зависимость импульса частицы от времени описывается законом 
, где и — единичные векторы координатных осей X, Y соответственно. Зависимость горизонтальной проекции силы , действующей на частицу, от времени представлена на графике….
Решение: 
Сила , действующая на материальную точку, равна скорости изменения ее импульса В нашем случае , и, сравнивая , находим и . Проекция силы на ось ; следовательно, с течением времени горизонтальная составляющая силы не меняется.
№4На покоящееся тело массы кг налетает с некоторой скоростью тело массы кг. Сила, возникающая при взаимодействии тел, линейно -зависящая от времени, растет от 0 до значения за время c. а затем равномерно убывает до нуля за то же время Все движения происходят по одной прямой. Скорость первого тела массы в после взаимодействия равна …
Решение Поскольку на тело действует переменная сила, применим второй закон Ньютона в виде . Импульс силы равен изменению механического импульса. Импульс силы взаимодействия равен (интеграл можно найти вычислив площадь под графиком функции . Изменение механического импульса . Находим скорость первого тела массы m1 после взаимодействия
№ 5Модуль скорости автомобиля изменялся со временем,как показано на графике зависимости ). В момент времени автомобиль поднимался по участку дуги.
Направление результирующей всех сил,действующих на автомобиль в этот момент времени,правильно отображает вектор…
Решение:
В системе отсчета,связанной с Землей ,ускорение автомобиля и результирующая действующих на него сил связаны вторым законом Ньютона: . Полное ускорение — тангенциальная состовляющая ускорения, нормальная состовляющая ускорения.
Как следует из графика зависимости модуля скорости от времени,в момент модуль скорости автомобиля достигает максимального значения . Поскольку автомобиль движется в этот момент по криволинейному участку траектории ,то (см.
рисунок) и ее направление совпадает с напрвление вектора 3.
- Ответ: 3
- №6Автомобиль поднимается в гору по участку дуги с увеличивающейся по величине скоростью. Равнодействующая всех сил, действующих на автомобиль, ориентирована в направлении
- Ответ: 4
- №7Импульс материальной точки изменяется по закону (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 4 c, равен
- Решение:Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: . Тогда зависимость силы от времени имеет вид Модуль силы , и в момент времени t = 4 c
- №8Импульс материальной точки изменяется по закону (кг·м/с). Модуль силы (в Н), действующей на точку в момент времени t = 2 c, равен
Решение: Согласно второму закону Ньютона скорость изменения импульса материальной точки равна действующей на нее силе: .Тогда зависимость силы от времени имеет вид .
Ответ: 8
№9Диск вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. К ободу диска приложена сила , направленная по касательной. Правильно изображает направление момента силы вектор
- Ответ: 3
- №10Диск начинает вращаться вокруг неподвижной оси с постоянным угловым ускорением. Зависимость момента импульса диска от времени представлена на рисунке линией
- Ответ: B
- №11Диск вращается вокруг неподвижной оси с постоянной угловой скоростью. Зависимость момента импульса диска от времени представлена на рисунке линией
- Ответ: Е
- №12 Тонкостенный цилиндр массы m и радиуса R вращается под действием постоянного момента сил вокруг оси, проходящей через центр масс цилиндра и перпендикулярной плоскости его основания. Если ось вращения перенести параллельно на край цилиндра, то (при неизменном моменте сил) его угловое ускорение …
- Ответ: уменьшится в 2 раза
- …
- №13Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.
- Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение
Решение: Момент инерции сплошного однородного кругового цилиндра (диска) массы m и радиуса R относительно его оси вычисляется по формуле , тонкостенного кругового цилиндра массы m и радиуса R относительно его оси – по формуле . Из последней формулы видно, что момент инерции тонкостенного цилиндра (трубы, кольца) не зависит от его высоты. Поэтому правильным для моментов инерции рассматриваемых тел относительно указанных осей является соотношение
№14Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил ( или ), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение
Решение: При вращении тела вокруг неподвижной оси момент относительно этой оси создает только одна составляющая действующей на него силы, а именно касательная к траектории точки ее приложения .
Тогда момент силы относительно неподвижной оси равен: , где r – радиус-вектор точки приложения силы. В данном случае составляющая одинакова для трех сил: а для силы . Кроме того, все силы приложены в одной точке.
Поэтому .
№15При выстреле орудия снаряд вылетел из ствола с угловой скоростью под углом к горизонту. Момент инерции снаряда относительно его продольной оси , расстояние между колесами орудия , время движения снаряда в стволе время выстрела, отличаются на …
Решение: Найдем угловые ускорения снаряда относительно продольной оси при выстреле . Со стороны ствола орудия на снаряд действует момент сил .
По третьему закону Ньютона такой же по модулю, но противоположно направленный момент сил действует на ствол орудия.
Его проекция на горизонтальную плоскость уравновешивается моментом, возникающим за счет различия сил реакций опоры (давление земли), действующих на колеса, , где — разность сил реакций опор. Отсюда находим . Вычисляем .
№16Шар, цилиндр (сплошной) и тонкостенный цилиндр с равными массами и радиусами раскрутили каждый вокруг своей оси до одной и той же угловой скорости и приложили одинаковый тормозящий момент. Раньше других тел остановится …
Решение.
При одинаковом моменте сил угловое ускорение обратно пропорционально моменту инерции тела. Момент инерции шара , момент инерции цилиндра , момент инерции тонкостенного цилиндра . Следовательно, ускорение торможения будет большим для шара и первым остановится шар.
№17 Тонкостенный цилиндр массы m и радиуса R вращается под действием постоянного момента сил вокруг оси, проходящей через центр масс цилиндра и перпендикулярной плоскости его основания. Если ось вращения перенести параллельно на край цилиндра, то (при неизменном моменте сил) его угловое ускорение …
Решение: Момент инерции при неизменных материале, форме и размерах тела зависит от расположения оси вращения. Момент инерции тонкостенного кругового цилиндра массы m и радиуса R относительно его оси . При переносе оси момент инерции тела изменится.
В соответствии с теоремой Штейнера + . Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси, угловое ускорение равно: .
Отсюда при неизменном моменте сил, действующих на тело, угловое ускорение цилиндра уменьшится в два раза.
№18Величина момента импульса тела относительно неподвижной оси изменяется по закону при этом зависимость величины момента сил, действующих на тело, описывается графиком…
Решение:
Скорость изменения момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е. где L-величина момента импульса,M –величина момента сил.
Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента сил от времени . Графиком этой функции является убывающая ветвь параболы.
№19Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором в точку 2 с радиус-вектором . При этом на нее действовала сила (радиус-векторы , и сила заданы в единицах СИ). Работа, совершенная силой , равна
Решение: По определению . С учетом того, что ,
№20Частица совершила перемещение по некоторой траектории из точки M (1, 2) в точку N (2, –1). При этом на нее действовала сила (координаты точек и сила заданы в единицах СИ). Работа, совершенная силой (в Дж), равна …
- Решение: По определению . С учетом того, что ,
- № 21 Мальчик тянет санки массой m по горизонтальной поверхности с ускорением , при этом веревка натягивается силой под углом к горизонту. Если коэффициент трения полозьев о поверхность равен , то уравнение движения санок в проекции на направление движения санок имеет вид …
- Ответ:
№22На рисунке приведен график зависимости скорости тела от времени t. Масса тела 20 кг. Сила (в H), действующая на тело, равна
Ответ:20
Работа. Энергия
№1На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела L1 = 0,1 Дж·с. Если m = 1 кг, R = 10см, то кинетическая энергия второго тела (в мДж) равна
Ответ: 250
№2Тело массы m=100г бросили с поверхности земли с начальной скоростью v0 = 10 м/с под углом α = 30° к горизонту. Если пренебречь сопротивлением воздуха, средняя мощность, развиваемая силой тяжести за время падения тела на землю, равна …
Решение: Средняя мощность, развиваемая силой за некоторый промежуток времени, равна отношению работы, совершаемой силой за рассматриваемый промежуток времени, к длительности этого промежутка: Работа силы тяжести и по условию задачи. Тогда A = 0 и, следовательно, средняя мощность, развиваемая силой тяжести за время падения тела на землю, также равна нулю.
- Ответ: 0
- №3Потенциальная энергия частицы задается функцией . — компонента (в Н) вектора силы, действующей на частицу в точке А(1, 2, 3), равна
- (Функция и координаты точки А заданы в единицах СИ.)
Решение:Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид , или , , . Таким образом, .
- Ответ: 6
- №4Потенциальная энергия частицы задается функцией . — компонента (в Н) вектора силы, действующей на частицу в точке А(1, 2, 3), равна
- (Функция и координаты точки А заданы в единицах СИ.)
- Ответ: -4
- №5Частица движется в двумерном поле, причем ее потенциальная энергия задается функцией . Работа сил поля (в Дж) по перемещению частицы из точки С (1, 1, 1) в точку В (2, 2, 2) равна …
- Решение: Дж
- №6Тело движется вдоль оси под действием силы, зависимость которой от координаты представлена на рисунке. Работа силы на пути определяется выражением …
- Решение:
Работа переменной силы в случае одномерного движения на участке определяется как интеграл: . На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:
.
№7Тело массы поднимают по наклонной плоскости. Высота наклонной плоскости м, длина ее основания м, коэффициент трения . Минимальная работа, которую надо совершить, в джоулях равна …
Решение: Минимальная сила, которую надо приложить к телу, чтобы поднимать его по наклонной плоскости без ускорения, равна сумме составляющей силы тяжести, параллельной наклонной плоскости, и силы трения: . Работа равна , где – длина наклонной плоскости. Учитывая, что и , получим . Следовательно,
- минимальная работа 14 Дж.
- №8На рисунке показан график зависимости потенциальной энергии от координаты х. График зависимости проекции силы F(x)от координаты х имеет вид…
- Решение:
- Потенциальная энергия ,как видно из графика, пропорциональна квадрату координаты — коэфициент пропорциональности. Проекция силы F(x)на ось Х связана с потенциальной энергией соотношением и равна
- График зависимости имеет вид
№9 Тело массой m=100 г бросили с поверхности земли вверх с начальной скоростью . Высота подъема тела оказалась равной м. Работа силы сопротивления (в Дж) воздуха равна …
Решение:Работа силы сопротивления воздуха равна изменению полной энергии тела: .
Разбор 30 задач по физике. Механика, Термодинамика и МКТ
При работе со своими учениками, у меня накапливается много задач.
Поэтому я публикую разборы задач в свободный доступ, стараюсь делать это максимально подробно и понятно, чтобы начинающие могли прочитать и разобраться в нужной для них теме.
Ну а за подробными индивидуальными консультациями и репетиторством вы можете написать в мою группу в вк или в личные сообщения. Также большое количество разборов задач вы сможете найти в моей группе Репетитор IT mentor
Задача 1
. На тело массой 100 кг, лежащее на наклонной плоскости, которая образует с горизонтом угол 40°, действует горизонтальная сила 1500 Н. Определить:1) силу, прижимающую тело к плоскости;2) силу трения тела о плоскость;
3) ускорение, с которым поднимается тело. Коэффициент трения k = 0.10; g = 10м/с².
Задача 2. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение тела, если на него действует сила тяжести P, а коэффициент трения между телом и плоскостью равен k . При какой величине силы F движение будет равномерным.
Задача 3
. Два шара массами m1 = 2.5 кг и m2 = 1.5 кг движутся навстречу друг другу со скоростями v1 = 6 м/c и v2 = 2 м/c . Определить: 1) скорости шаров после удара; 2) кинетические энергии шаров до и после удара; 3)энергию, затраченную на деформацию шаров при ударе. Удар считать прямым, неупругим.
Прикрепляю очередной разбор задачи по физике по теме закона сохранения импульса. Неупругие шары после удара не восстанавливают свою первоначальную форму. Таким образом, сил, которые отталкивали бы шары друг от друга, не возникает. Это значит, что после удара шары будут двигаться вместе (слипшись) с одной и той же скоростью .
Эту скорость определим по закону сохранения импульса. Так как шары двигаются по одной прямой, то можно записать импульс системы до удара и после удара. Считаем, что в задаче не действует диссипативных сил (сил трения, сопротивления воздуха и т.д.), поэтому импульс вдоль оси Ox сохраняется, тогда (смотри решение на картинке).
Расписал довольно подробно, но если что-то не будет понятно, то задавайте вопросы в х.
Задача 4. Диск массой m, радиус которого R , вращается с угловой скоростью ω0 вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. После прекращения действия на него силы диск останавливается в течение времени t. Определить угловое ускорение диска и тормозящий момент, действующий на него.
Задача 5. Два тела массами m1 и m2 связаны нитью, перекинутой через блок массой M . Найти ускорение тел, считая блок сплошным диском.
Задача 6. Шар катится по горизонтальной поверхности со скоростью v . На какую высоту h относительно своего первоначального положения поднимется шар, если он начнет вкатываться на наклонную плоскость без проскальзывания?
Задача 7. На краю вращающейся с угловой скоростью ω0 платформе стоит человек массой m. После того, как человек перешёл в другую точку платформы, угловая скорость её вращения стала равной ω. Найти расстояние от оси вращения до человека, считая платформу диском массой M и радиусом R.
Задача 8. Тело массой m брошено со скоростью v0 под углом α к горизонту. Найти кинетическую и потенциальную энергию тела в высшей точке траектории.
Задача 9. На горизонтальной поверхности находятся два тела массами m1 = 10 кг и m2 =15 кг, связанные нитью. К телу массой m2 прикладывают силу F = 100 Н, направленную под углом α = 60° к горизонту. Определить ускорение грузов и силу натяжения нити, соединяющей грузы. Трением пренебречь. (обязательно указать все силы на чертеже!)
Задача 10. На поверхности стола лежит груз массой m2 = 2 кг. На нити, прикрепленной к грузу m2 и перекинутой через невесомый блок, подвешен груз m1 = 1 кг. Коэффициент трения груза о поверхность стола 0,2. Найти ускорение грузов и силу натяжения нити.
Задача 11
. Лодка массой 200 кг и длиной 3 м стоит неподвижно в стоячей воде. Мальчик массой 40 кг в лодке переходит с носа на корму. Определите, на какое расстояние при этом сдвинется лодка.
Считаем, что в нашей задаче не действует внешних сил, поэтому по теореме о центре массы системы грузов, можно считать, что координаты центра масс сохраняются в проекциях на ось OX (по оси OY движения не происходит). Проведем ось Y(ноль оси X) через центр лодки, тогда можно записать координаты человека и лодки до перехода человека с носа на корму.
Задача 12. Шарик массой 5 кг подвешен на нити. Нить может выдержать максимальное натяжение 100 Н. На какой минимальный угол от положения равновесия нужно отклонить нить с шариком, чтобы он оборвал нить, проходя через положение равновесия? (обязательно сделать рисунок, указать действующие силы!)
Задача 13. Два неупругих шара массами m1=2 кг и m2=3 кг движутся со скоростями соответственно v1=8 м/c и v2=4м/с. Определить количество теплоты, выделившееся при их столкновении. Рассмотреть 2 случая: 1) шары движутся навстречу друг другу; 2) меньший шар догоняет больший.
Задача 14. Тело совершает гармонические колебания по закону x(t) = 50⋅sin(π/3⋅t) (см). Определить полную энергию тела, если его масса 0,2 кг. Какая сила действует на тело в момент времени t = 0,5 с?
Задача 15. Два математических маятника, длины которых отличаются на Δℓ =16 см, совершают за одно и то же время: один − 10 колебаний, другой − 6 колебаний. Определить длины маятников.
Задача 16. Определить, сколько молей и молекул водорода содержится в объёме V = 5 м³ под давлением Р = 767 мм.рт.ст. при температуре t = 18 ° С. Какова плотность газа?
Задача 17. Сколько кислорода выпустили из баллона ёмкостью 1 дм3, если давление его изменилось от 14 атм до 7 атм, а температура от 27°С до 7 °С ?
Задача 18. В сосуде объёмом V = 2 м³ находится смесь m1 = 4 кг гелия и m2 = 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.
Задача 19. В сосуде содержится смесь газов: гелия массой 12 г и водорода массой 2 г, температура в сосуде 77°С, давление 20 кПа. Определить молярную массу и плотность смеси газов.
Задача 20. Гелий массой 20 г нагрели от 100°С до 400°С, причем газу была передана теплота 30 кДж. Найти изменение внутренней энергии гелия и совершенную им работу.
Задача 21. При изотермическом расширении от 0,1 м3 трех молей газа его давление меняется от 4,48 атм до 1 атм. Найти совершаемую при этом работу и температуру, при которой протекает процесс.
Задача 22. Моль идеального газа, имевший первоначально температуру 300ºК, расширяется изобарически до тех пор, пока его объем не возрастет в 3 раза. Затем газ охлаждается изохорически до первоначальной температуры. Определить суммарное получаемое газом количество теплоты. Обязательно нарисовать графики процессов.
Задача 23. Азот массой m = 1 кг занимает при температуре Т1 = 300 К объём V = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить конечный объём газа и конечную температуру.
Задача 24. Газ расширяется адиабатически, причём объём его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы этого газа?
Задача 25. Баллон ёмкостью V = 20 л с кислородом при давлении Р = 107 Па и температуре t1 = 70 ºС нагревается до температуры t2 = 270 ºС. Какое количество теплоты при этом поглощает газ?
Задача 26. Азот, занимающий при давлении, равном Р1 = 10⁵ Па объём V1 = 10 л, расширяется вдвое. Найти конечное давление и работу, совершённую газом в процессах: а) изобарном; б) изотермическом; в) адиабатном.
Задача 27. Кислород, масса которого 200 г, нагревают от температуры Т1 =300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы и близки к атмосферному.
Задача 28. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 1,5∙10⁵ Дж. Температура нагревателя Т1 = 400 К, температура холодильника Т2 = 260 К. Найти КПД машины, количество теплоты Q1, получаемое машиной за один цикл от нагревателя, и количество теплоты Q2, отдаваемое за один цикл холодильнику.
Задача 29. Найти суммарную кинетическую энергию Е поступательного движения всех молекул, содержащихся в объёме V = 1 дм³ газа при атмосферном давлении.
Задача 30. Чему равны средние кинетические энергии поступательного и вращательного движения молекул, содержащихся в 100 г водорода при температуре 400 К ? Чему равна полная внутренняя энергия газа?
- Спасибо, что дочитали до конца, дорогие подписчики 🙂 Если вам интересен подобный контент и разборы задач, то оставляйте обратную связь в виде лайков и комментариев.
- Еще много полезного и интересного вы сможете найти на ресурсах:Репетитор IT mentor в VK
- Репетитор IT mentor в Instagram
- Репетитор IT mentor в Telegram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
ПОИСК
Помимо названных схем в практике расчетов используют также и другие простейшие схемы, например сплошной цилиндр, тонкостенный цилиндр. В приведенных схемах тел могут использоваться как декартовы, так и цилиндрические или полярные координаты.
[c.141]
- Цилиндры тонкостенные с отверстием —
[c.562] - Цилиндры тонкостенные с отверстием — Коэффициент концентрации—Формулы расчетные 407 Цинк—Коэффициент Пуассона 22
[c.562] - Цилиндры тонкостенные с отверстием — Коэффициент концентрации — Формулы расчетные 3 — 407
[c.493]
Валы контролируются жесткими предельными калибрами-скобами.
Калибры-кольца применяются только для контроля небольших коротких цилиндров, тонкостенных изделий и тонких штифтов (цапф).
[c.485]
Передача состоит из трех кинематических звеньев (рис. 15.1) гибкого колеса g, жесткого колеса Ь и генератора волн Н. Гибкое колесо g выполняют в виде цилиндра, на кольцевом утолщении которого нарезаны наружные зубья.
Гибкий тонкостенный цилиндр выполняет роль упругой связи между деформируемым кольцевым утолщением и жестким элементом передачи, которым может быть выходной вал (рис. 15.1, а) или корпус (рис. 15.1, б, в). Жесткое колесо Ь — обычное зубчатое колесо с внутренними зубьями. Генератор Ь волн деформации представляет собой водило (например, с двумя роликами), вставленное в гибкое колесо.
При этом гибкое колесо, деформируясь в форме эллипса, образует по
[c.234]
При закреплении тонкостенных втулок, колец, гильз и т. п. в трехкулачковом патроне для обработки отверстия их цилиндрическая форма искажается от сил зажатия. Такие детали, будучи обработаны в деформированном состоянии, после освобождения из патрона принимают первоначальную форму, вследствие чего обработанное отверстие теряет форму окружности и цилиндра.
[c.60]
Задача I—23. Тонкостенный сосуд, состоящий из двух цилиндров диаметрами с1 0,3 м и = 0,8 м, нижним открытым концом опущен под уровень воды в резе]ь вуаре А и покоится на опорах С, расположенных на высоте Ь = 1,5 м над этим уровнем.
[c.25]
Задача 1—27, Тонкостенный сосуд А высотой Н = = 60 мм и диаметром (1 = 24 мм с отверстием внизу плавает в воде, содержащейся в цилиндре диаметром В = = 72 мм.
[c.27]
Задача 1—31. Прессовый прибор для создания малых избыточных давлений воздуха состоит из трех тонкостенных цилиндров одинаковой высоты а = 250 мм.
Цилиндры диаметрами Ох = 100 мм и Оз = 200 мм неподвижны кольцевое пространство между ними до уровня Яо заполнено водой.
Цилиндр диаметром О-х = 150 мм, перемещаясь по вертикали с помощью винта, опускается нижней кромкой под уровень воды и, сжимая отсеченный в приборе объем воздуха повышает его давление.
[c.30]
Задача III—8. Горизонтальный цилиндрический сосуд диаметром d = 0,8 м с полусферической и конической тонкостенными крышками заполнен жидкостью плотностью pi. Правая половина цилиндра (с конической крышкой) вставлена в замкнутый резервуар и находится
[c.61]
Тонкостенным сосудам обычно придают форму цилиндра, сферы или тора (рис. 8.25, а—в). Выбор формы может определяться различными соображениями. Сферический сосуд при заданной емкости
[c.260]
При расчете тонкостенных цилиндров предполагается, что в окружном направлении напряжения постоянны по толщине стенки, а в радиальном вообще отсутствуют. Эти допущения неприемлемы для толстостенных цилиндров.
[c.443]
Допустим, что к тонкостенному длинному цилиндру (рис. 483) в сечении А — А приложена равномерно распределенная по периметру сечения нагрузка интенсивностью q кгс/см. В данном случае краевой эффект симметричен относительно линии АА. Поэтому [c.485]
Заметим, что в силу тонкостенности кольца, представляющего собой сечение цилиндра, по которому действуют напряжения 02, площадь его подсчитана как произведение длины окружности на толщину стенки.
[c.262]
Сказанное находит свое подтверждение в проведенном выше расчете цилиндрического сосуда (см. 61), где было показано, что в случае тонкостенного цилиндра окружное напряжение можно считать равномерно распределенным по толщине. Радиальное напряжение при малой толщине оказалось пренебрежимо малым по сравнению с окружным из-за большой величины последнего.
[c.294]
Сначала остановимся на простейших вопросах безмоментной теории. Далее будут рассмотрены задачи, связанные с определением изгибных напряжений в простейших случаях нагружения пластин и тонкостенного цилиндра.
[c.294]
Круговой тонкостенный цилиндр радиуса Я и постоянной толщины 1 находится под действием некоторой осесимметричной нагрузки
[c.315]
При больших размерах цилиндра (диаметр и длина) процесс распространения теплоты аналогичен процессу в бесконечной пластине. Однако при малых диаметрах происходит наложение тепловых потоков от различных участков выполняемого шва.
Рассмотрим общий случай нагрева тонкостенного цилиндра источником, который начинает свое движение из точки О (рис. 6.19,а) под некоторым углом а к образующей цилиндра достаточно большой длины.
Процесс распространения теплоты в цилиндре диаметром d в этом случае аналогичен случаю одновременного движения бесконечно большого числа источников теплоты из точек 0 , О2,. .., On, сдвинутых относительно друг друга на шаг nd (рис. 6.19,6).
Температурное поле достаточно рассматривать в пределах одного интервала nd, так как оно будет повторяться во всех других интервалах.
[c.189]
Вариант 16. Вагонетка I общей массой wii = 6500 кг, движущаяся по горизонтальному прямолинейному пути, наталкивается на неподвижную тележку 2, имеющую вместе с грузом массу 12 = 4000 кг. Груз-однородный полый тонкостенный цилиндр массой Шо = 500 кг и радиусом г = 0,5 м — удерживается от возможного перемещения по тележке двумя упорами — ступеньками.
[c.225]
При внезапной остановке оси подвеса маятник, находясь в том же положении и приобретя угловую скорость, ударяется точкой Е о неподвижный однородный полый тонкостенный цилиндр радиусом г = 0,2 м и массой III = 2)По.
Коэффициент восстановления при соударении тел к = 1/3. Поверхности маятника и цилиндра в точке соударения — гладкие. Плоскость, на которой покоится цилиндр, абсолютно шероховата, т. е. не допускает скольжения тела при ударном воздействии.
[c.225]
Вариант 29. Маятник, отклоненный от положения устойчивого равновесия на некоторый угол а, падает без начальной скорости под действием собственного веса, вращаясь вокруг неподвижной оси О, и в вертикальном положении точкой А ударяется о покоящийся однородный полый тонкостенный цилиндр массой diq = 200 кг и радиусом г = 0,2 м.
[c.229]
Па. Схема установки представлена на рис, 6-31, Покрытие наносилось на тонкостенный металлический цилиндр, который разогревался нагревателем, помещенным внутри цилиндра.
[c.169]
Задача 1071 (рис. 527). По двум параллельным горизонтальным рейкам катится без скольжения тонкостенный цилиндр массой А1 при помощи груза, подвешенного на нити, намотанной на цилиндр.
[c.372]
Задача 1246 (рис. 662). На гладкой горизонтальной плоскости находится доска массой ш- , а на доске—тонкостенный цилиндр массой т . Предполагая, что скольжение между цилиндром и доской отсутствует, определить величины абсолютных ускорений доски и оси цилиндра w , если к доске приложена сила G.
[c.442]
Задача 1256 (рис. 672). Система состоит из призмы А и тонкостенного цилиндра В, масса которого в 3 раза меньше массы призмы.
Цилиндр обмотан гибкой нерастяжимой нитью, закрепленной на призме так, что участок нити ВС параллелен линии наибольшего ската наклонной грани призмы.
Определить ускорение призмы и ускорение оси цилиндра по отношению к призме, если угол наклона грани к горизонту ф = 45°.
[c.445]
Задача 1258 (рис. 674). Тонкостенный цилиндр А массой т н груз В массой mj, соединенные между собой посредством нити, конец которой намотан на цилиндр, положены на стороны неподвижной гладкой призмы, как указано на рисунке. Найти ускорения груза и оси цилиндра, пренебрегая массой блока С, если углы, образуемые гранями призмы с горизонтом, соответственно равны аир. При каком соотношении масс цилиндр будет вра-
[c.446]
Задача 1262 (рис. 676). На гладкой призме, помещенной на гладкой горизонтальной плоскости, находится тонкостенный цилиндр А с намотанной на него нитью, к концу которой привязан груз М, как указано на рисунке. Считая, что массы цилиндра и груза равны между собой, определить ускорение призмы, если угол а = 45°. В начальный момент система была в покое.
[c.447]
Задача 1265 (рис. 678). Через блок А перекинута нить, один конец которой прикреплен к блоку В, а другой навит на тонкостенный цилиндр С с массой т. , имеющий свободную ось. Через блок В также перекинута нить, несущая грузы и с массами, равными и т.
, соответственно. Определить ускорения грузов и оси цилиндра (по отношению к неподвижному основанию прибора), если т = 2 кг кг т = 2 кг. Массами блоков и нитей, а также трением в осях пренебречь. В начальный момент система находилась в покое.
[c.
448]
Задача 1266 (рис. 679). На гладких гранях призмы, которая может скользить без трения по горизонтальной поверхности, находятся груз Ли тонкостенный цилиндр В, свя-занные между собой посредством нити, пере- /3 кинутой через идеальный блок, конец кото-
[c.448]
БИМЕТАЛЛИЧЕСКИЕ ЦИЛИНДРЫ Тонкостенная труба испытывает нагрузки внутреннее давление q, осевую силу N (на единицу длины, полную осевую силу lurN), температурные деформации
[c.246]
Минимальная величина жидкостных зазоров может быть выбрана по условиям вязкости жидкости и засоряемости зазоров. К этому же минимуму необходимо стремиться и по условию прочности.
Так как напряжения в цилиндрах (тонкостенных) возрастают пропорционально радиусу, то чем меньше зазор, тем меньше радиус внешних цилиндров, тем меньше напряжения в стенках цилиндров.
Величина жидкостного зазора может быть порядка 5—10 м..
[c.21]
Цилиндры тонкостенные 20Х Токарно-винторезный станок 63С 8 ПП 150X40X32 35 7 9
[c.62]
На деталях, обрабатываемых в патроне (рис. 6.103, б), следует предусматривать такие поверхности 7, которые обеспечивают правильную установку и надежное закрепление при обработке. Наиболее надежно закрепление по поверхностям в виде к1)уговых цилиндров.
Поверхности точно обрабатываемых отверстий также следует разделять введением выточек. Предпочтительнее жесткие детали. Закрепление в патронах тонкостенных (нежестких) деталей может вызвать большие деформации и снизить точность.
Шлифование отверс 1ий малых диаметров связано с трудностями и должно назначаться в исключительных случаях.
[c.371]
Передача состоит из т )ех кинематических звеньев (рис. 15.1) ih6koio колеса g, жесткого колеса h н генера тора волн h. Гибкое колесо g выполняют в виде цилиндра, на кольцевом утолщении которого нарезаны наружные зубья.
Гибкий тонкостенный цилиндр выполняет роль упругой связи между деформируемым кольцевым утолщением и жестким элементом передачи, которым может 6i>irr. m.ixu i,Hoii ва.п (рис. 15.1, и) или koihiv (рис-. 15.1,6, в). Жесткое колесо Ь обычное зубчатое ко.
,лесо с внутренними зубьями.
[c.209]
Задача I—26. Для измерения малых сил используется дшдкостиый динамометр, состоящий из цилиндра Л, наполненного до некоторого уровня ртутью, и погруженного в ртуть тонкостенного поршня В. Пространство под поршнем заполнено спиртом (б = 0,8) и соединено с трубкой
[c.26]
Простейший конденсационный гигрометр состоит из металлического тонкостенного цилиндрического сосуда, стенки которого тщательно отполированы. Сосуд заполняется эфиром. Если через эфир прокачивать воздух, то часть эфира испарится и температура его понизится.
Практически температура эфира равна температуре стенок цилиндра. Охлаждение эфира производят до тех пор, пока на полированной металлической поверхности сосуда не появится роса.
В этот момент замечанзт температуру эфира, которая будет соответствовать температуре точки росы. Появление росы свидетельствует о переходе прилегающего слоя воздуха у стенок сосуда в состояние насыщения.
Пользуясь таблицами для насыщенного водяного пара, можно по температуре точки росы определить парциальное давление водяного пара во влажном воздухе.
[c.240]
Если внутренний радиус цилиндра а будет малым, то посадка труб по соотношениям Гадолина дает почти двукратное снижение эквивалентного напряжения. Для тонкостенных труб, т. е. при а яа й, посадка труб не дает эффекта.
[c.286]
Рассмотрим задачу об определении напряжений в симметрично нагруженном тонкостенном цилиндре. Эта задача решается при тех же допущениях, что и задача об изгибе пластин, т. е. принимается гипотеза неизменности нормали и предположение о ненадавливании слоев оболочки друг на друга.
[c.315]
Нагрев при однопроходной дуговой сварке продольных и кольцевых швов тонкостенных цилиндрических оболочек, несмотря на их кривизну, может быть приравнен к случаю нагрева пластины линейным источником теплоты. Это объясняется тем, что цилиндр представляет собой развертываюш,уся поверхность.
[c.189]
При винтовой наплавке на тонкостенный цилиндр (рис. 6.19,г) можно также приближенно пользоваться схемой быстродвижу-щегося линейного источника теплоты в пластине с суммированием температурных полей от отдельных источников. Если приближенно полагать а ж 90°, то
[c.191]
Тонкостенным сосудам обычно придают форму сферы, цилиндра или тора (рис. 1.4, а-в). Выбор формы может определяться различными соображениями.
Сферический сосуд при заданной емкости (объеме) имеет минимальную массу, оровый можно наиболее компактно разместить, а цилиндрическая форма сосуда обеспечивает наиболее технологичное конструктивное оформление.
Соединения основных элементов сосуда (аппарата) осуществляют продольными, кольцевыми и круговыми швами.
[c.17]
Вариант 22. Груз — однородный полый тонкостенный цилиндр массой т = 800 кг и pamiy oM г = 0,4 м — покоится на движущейся платформе между упорами — ступеньками.
При внезапной остановке платформы ступенька АВ не удерживает груз цилиндр, поднимаясь на ступеньку, прокатывается по участку BD = s = 1 м горизонтальной площадки BE и, ударившись о ребро F другого упора — ступеньки EF высотой
[c.226]
Груз — однородный полый тонкостенный цилиндр массой Wq = 500 кг и радиусом г = 0,5 м — удерживается от возможного перемещения по тележке двумя угюрами — наклонными плоскостями.
[c.228]
Загрузка...
