Характеристика гидравлического сопротивления трубопровода

ГлавнаяСтатьи и материалыГидравлическое сопротивление труб

Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги.

А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление.

Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.

Гидравлический расчёт выполняется с целью:

• Вычисления потерь давления на конкретных отрезках системы отопления;
• Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
• Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
• Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.

Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса.

Только правильные расчёты помогут выбрать оптимальный вариант насоса.

Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.

А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.

• Это безмерная величина, показывающая, каковы потери удельной энергии.
• Ламинарное перемещение рабочего потока
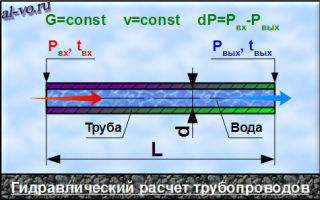
• При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:

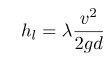
1. Где:
2.  — потери давления по длине;
3.  — коэффициент гидравлического сопротивления;
4. v – скорость движения рабочей среды;
5. g – ускорение силы тяжести;
6. d – диаметр трубопроводной магистрали.
7. Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.
8. Если Re меньше, чем 2300, то для расчёта применяется формула:
9. Для трубопроводов в форме круглого цилиндра:
10. Для трубопроводных коммуникаций с другим (не круглым) сечением:
11. Где А=57 – для квадратных труб.
12. Турбулентное течение рабочего потока
13. При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при

• В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.
• Коэффициент местного сопротивления
• Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:

1. Где:
2.  – коэффициент местного сопротивления;
3.  – потеря напора;
4.  – отношение скорости потока к ускорению силы тяжести – скоростной поток.
5. При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:

 – энергия торможения.

Для фитингов из ППР:

ДетальОбозначениеПримечаниеКоэффициент

Муфта	0,25
Муфта переходная	Уменьшение на 1 размер	0,40
Уменьшение на 2 размер	0,50
Уменьшение на 3 размер	0,60
Уменьшение на 4 размер	0,70
Угольник 90°	1,20
Угольник 45°	0,50
Тройник	Разделение потока	1,20
Соединение потока	0,80
Крестовина	Соединение потока	2,10
Разделение потока	3,70
Муфта комб. вн. рез.	0,50
Муфта комб. нар. рез	0,70
Угольник комб. вн. рез.	1,40
Угольник комб. нар. рез.	1,60
Тройник комб. вн. рез.	1,40 — 1,80
Вентиль	20 мм	9,50
25 мм	8,50
32 мм	7,60
40 мм	5,70

Для полиэтиленовых труб

ТрубаРасход, м3/часСкорость, м/сПотери напора в метрах, на 100 метров прямого трубопровода (м/100м)

Сталь новая 133×5	60	1,4	3,6
Сталь старая 133×5	60	1,4	6,84
ПЭ 100 110×6,6 (5ЭР 17)/td>	60	2,26	4,1
ПЭ 80 110×8,1 (ЗйР 13,6)	60	2,41	4,8
Сталь новая 245×6	400	2,6	4,3
Сталь старая 245×6	400	2,6	7,0
ПЭ 100 225×13,4 (50 В 17)	400	3,6	4,0
ПЭ 80 225×16,6 (ЗЭК 13,6)	400	3,85	4,8
Сталь новая 630×10	3000	2,85	1,33
Сталь старая 630×10	3000	2,85	1,98
ПЭ 100 560×33,2 (ЗЭК 17)	3000	4,35	1,96
ПЭ 80 560×41,2 (ЗЭК 13,6)	3000	4,65	2,3
Сталь новая 820×12	4000	2,23	0,6
Сталь старая 820×12	4000	2,23	0,87
ПЭ100 800×47,4 (ЗЭК 17)	4000	2,85	0,59
ПЭ 80 800×58,8 (ЗЭР 13,6)	4000	3,0	0,69

Для бесшовных стальных труб

Режим движенияЧисло РейнольдсаОпределения λ

Ламинарный	или
Переходный		Проектирование трубопроводов не рекомендуется
Турбулентный	1-я область	(ф-ла Блазиуса) Бф-ла Конакова)
2-я область		(ф-ла Альтшуля)
3-я область	(ф-ла Альтшуля) (ф-ла Никурадзе)

Для металлопластиковых труб

НаименованиеСимволКоэффициент

Тройник разделения потока	7,6
Тройник проходной	4,2
Тройник противоположные потоки при разделении потока	8,5
Тройник противоположные потоки при слиянии потока	8,5
Угол 90°	6,3
Дуга	0,9
Редукционный переход	6,3
Установочный уголок	5,4

С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:

Пластиковые трубы произведенные в Германии, широкого спектра применения.

Система отлично подходит для систем горячего и холодного водоснабжения и отопления, как в частных, так и промышленных масштабах. Так же используется для транспортировки химических сред.

Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.

• Пластиковые трубы произведенные в Германии, широкого спектра применения.
• Трубопроводная система из инновационного материала fusiolen, специально разработанная для систем холодоснабжения, обогрева поверхностей, транспортировки агрессивных сред и сжатого воздуха, а также для систем геотермальной энергетики.
• Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.

Помогите рассчитать потерю давления на газопроводе с начальным диаметром dn80, через 0,1 м становиться dn32 и тянется 10 м Уважаемый Андрей! Информация направлена на вашу почту! Добрый день, помогите рассчитать сопротивление резиновых трубопроводов. Уважаемый Николай! Информация направлена на Вашу почту. Что такое м/100м (в потерях напора)? Уважаемый Павел! Данная колонка с данными отображает потери напора в метрах, на 100 метров прямого трубопровода (м/100м).

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Коэффициент гидравлического сопротивления

• Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:
• Δh= ΔP/(ρg)
• где ρ — плотность среды, g — ускорение свободного падения.
• В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:   Поворотов   Диафрагм   Задвижек   Вентилей   Кранов   Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

1. Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.
2. hr = ξ υ2 / (2g)
3. где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет.

В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач.

Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

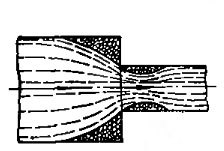
Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

ξвн. суж = 0,5(1- (F2/F1))

Значение коэффициента ξвн. суж от значения отношения (F2/F1)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

• В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле
• ξ поворот = 0,946sin(α/2) + 2.047sin(α/2)2
• где α – угол поворота трубопровода.
• Местные гидравлические сопротивления при входе в трубу

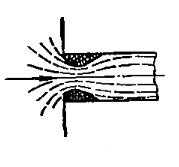
В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали.

Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение.

Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

1. Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:
2. ξвх = 0,505 + 0,303sin α + 0,223 sin α2
3. Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

• Гидравлическое сопротивление полностью открытой запорной арматуры равно
• ξвентиля = от 2,9 до 4,5
• Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.
• Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:   режима движения жидкости   отношения диаметров отверстия диафрагмы и трубы   конструктивных особенностей диафрагмы.

1. Для диафрагмы с острыми краями:
2. ξдиафр = d02 / D02
3. Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

ξвхода = 1

Видео о гидравлическом сопротивлении

• На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)
• Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.
• Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

Вместе со статьей «Гидравлическое сопротивление» читают:

Гидравлическое сопротивление

Опубликовано 24 Июн 2018Рубрика: Теплотехника | 26 комментариев

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно  повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно.

В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати.

Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.

Краткая теория

В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.

• Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
• В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
• ∆Р=ζ·ρ·w²/2, Па, где:

• ζ – безразмерный коэффициент местного сопротивления;
• ρ – объёмная плотность жидкости, кг/м3;
• w – скорость потока жидкости, м/с.

Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!

Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.

1. В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:

∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:

• L – длина трубы, м;
• D – внутренний диаметр трубы, м;
• λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).

Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:

ζтр=λ·L/D

1. Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:

1. ∆Рм=ζм·ρ·w²/2, Па
2. Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
3. Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
4. w=G/(ρ·π·D²/4), м/с, где:

• G – расход жидкости, кг/с;
• π – число Пи.

• Тогда:
• ∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
• ∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
• Введем понятие гидравлических сопротивлений:
• Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
• Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
• И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
• ∆Ртр=Sтр·G², Па;
• ∆Рм=Sм·G², Па.
• Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м3/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.
• Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.
• Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
• Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
• Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
• ai=(1/Si)0,5, (кг/с)/Па0,5.

Коэффициент гидравлического трения

Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.

В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.

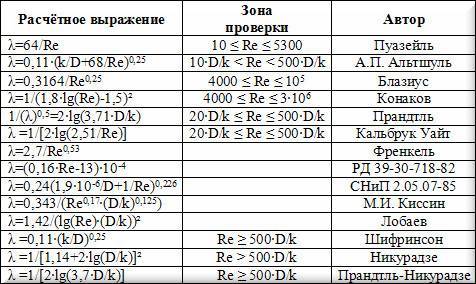
Обозначения в таблице:

• Re – число Рейнольдса;
• k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.

1. В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
2. λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
3. Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
4. Значения, полученные по этой формуле чрезвычайно близки значениям:

• функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10

Гидравлический расчет трубопровода — Проф Трубы

26.02.2019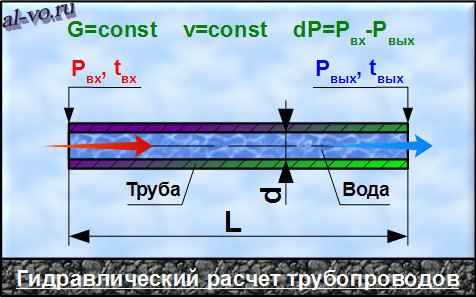

Содержание

• 1 Введение
• 2 Расчетная часть
• 3 Заключение

Трубопровод как способ транспортировки жидких и газообразных сред является самым экономичным способом во всех отраслях народного хозяйства. А значит он  всегда будет пользоваться повышенным вниманием у специалистов.

Гидравлический расчет при проектировании трубопроводной системы позволяет определить внутренний диаметр труб и падение напора в случае максимальной пропускной способности трубы. При этом обязательным является наличие следующих параметров: материал, из которого изготовлены трубы, вид трубы, производительность, физико-химические свойства перекачиваемых сред.

Производя вычисления по формулам, часть заданных величин можно взять из справочной литературы. Ф.А.Шевелев, профессор, доктор технических наук разработал таблицы для точного расчета пропускной способности.

Таблицы содержат значения внутреннего диаметра, удельного сопротивления и др параметры. Помимо этого, существует таблица приближенных значений скоростей для жидкостей, газа, водяного пара для упрощения работы с определением пропускной способности труб.

Используется в коммунальной сфере, где точные данные  не столь необходимы.

Способ установки гидравлических трубопроводов

Расчетная часть

• Расчет диаметра начинается с использования формулы равномерного движения жидкости (уравнение неразрывности):
• q = v*ω,
• где q — расчетный расход
• v — экономическая скорость течения.
• ω — площадь поперечного сечения круглой трубы с диаметром d.
• Рассчитывается по формуле:
• ω = πd² / 4,
• где d — внутренний диаметр
• отсюда  d = √4*q/ v*π

Скорость движения жидкости в трубопроводе принимается равной 1,5-2,5 м/с.

Это то значение, которое соответствует оптимальной работе линейной системы.

1. Потери напора (давления) в напорном трубопроводе находят по формуле Дарси:
2. h = λ*( L/ d)*( v2/2g),
3. Как проводится гидравлический расчет
4. где g — ускорение свободного падения,
5. L — длина участка трубы,
6. v2/2g — параметр, обозначающий скоростной (динамический) напор,

λ — коэффициент гидравлического сопротивления, зависит от режима движения жидкости и степени шероховатости стенок трубы. Шероховатость подразумевает неровность, дефект внутренней поверхности трубопровода и подразделяется на абсолютную и относительную. Абсолютная шероховатость — это высота неровностей. Относительную шероховатость можно рассчитать по формуле:

ε = е/r.

Шероховатость различна по форме и неравномерна по длине трубы. В связи с этим в расчетах принимается усредненная шероховатость k1 — поправочный коэффициент.

Данная величина зависит от целого ряда моментов: материал труб, длительность эксплуатации системы, различные дефекты в виде коррозии и др. При стальном исполнении трубопровода значение применяется равным 0,1-0,2 мм.

В то же время, в иных ситуациях параметр k1 можно взять из таблиц Ф.А.Шевелькова.

• В том случае, если длина магистрали невысока, то местные потери напора (давления) в оборудовании насосных станций примерно одинаковы потерям напора по длине труб. Общие потери определяются по формуле:
• h = P/ρ*g, где
• ρ — плотность среды

Случаются ситуации, когда трубопровод пересекает какое-либо препятствие, например, водные объекты, дороги и др. Тогда используются дюкеры — сооружения, представляющие собой короткие трубы, прокладываемые под преградой. Здесь тоже наблюдается напор жидкости. Диаметр дюкеров находится по формуле (с учетом, что скорость течения жидкости составляет более 1 м/сек):

1. h = λ*( L/ d)*( v2/2g),
2. h = I*L+ Σζ* v2/2g
3. ζ — коэффициент местного сопротивления

Разность отметок лотков труб в начале и конце дюкера принимается равной потерям напора.

• Материал для гидравлических трубопроводов
• Местные сопротивления рассчитываются по формуле:
• hм = ζ* v2/2g.

Движения жидкости бывают ламинарные и турбулентные. Коэффициент hм зависит от турбулентности потока (число Рейнольдса Re). С увеличением турбулентности создаются дополнительные завихрения жидкости, за счет чего величина коэффициента гидравлического сопротивления увеличивается. При Re › 3000 всегда наблюдается турбулентный режим.

Коэффициент гидравлического сопротивления при ламинарном режиме, когда Re ‹ 2300, рассчитывается по формуле:

λ = 64/ Re

В случае квадратичности турбулентного потока ζ будет зависеть от архитектуры линейного объекта: угла изгиба колена, степенью открытия задвижки, наличием обратного клапана. Для выхода из трубы ζ равна 1. Длинные трубопроводы имеют местные сопротивления порядка 10-15% на трение hтр. Тогда полные потери:

Производя расчеты, выбирается насос, исходя из параметров подачи, напора, действительной производительности.

Заключение

Гидравлический расчет трубопровода вполне возможно произвести в онлайн-ресурсе, где калькулятор выдаст искомую величину. Для этого достаточно ввести в качестве исходных величин состав труб, их длину и машина выдаст искомые данные (внутренний диаметр, потери напора, расход).

Помимо этого, существует онлайн версия программа «Таблицы Шевелева» ver 2.0. Она проста и удобна в освоении, является имитатором книжного варианта таблиц и также содержит калькулятор подсчета.

Компании, занимающиеся прокладкой линейных систем, имеют в своем арсенале специальные программы для расчетов пропускной способности труб. Одна из таких «Гидросистема» разработана российскими программистами, популярна в российской же промышленности.

Источник:

Самостоятельный гидравлический расчет трубопровода

Гидравлическое сопротивление трубопроводов

Виды гидравлических сопротивлений

Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная силе сопротивления, т. е. необходимо затрачивать энергию. Энергию или напор, необходимый для преодоления сил сопротивления, называют потерянной энергией или потерянным напором. Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение или потерь напора по длине потока (линейные потери напора) и обозначаются обычно hтр.

Однако трение является не единственной возможной причиной, вызывающей потери напора. Резкое изменение сечения также оказывает сопротивление движению жидкости (так называемое сопротивление формы) и вызывает потери энергии.

Существуют и другие причины, вызывающие потери напора, например внезапное изменение направления движения жидкости.

Потери напора, вызываемые резким изменением конфигурации границ потока (затрачиваемые на преодоление сопротивления формы), называют местными потерями напора или потерями напора на местные сопротивления и обозначаются через hм.

Таким образом, потери напора при движении жидкости складываются из потерь напора на трение и потерь на местные сопротивления, т. е.:

hS = hтр + hм.

***

Потери напора при равномерном движении жидкости в трубах

• Найдем общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов.
• При равномерном движении величина средней скорости и распределение скоростей по сечению остаются неизменными по всей длине трубопровода. Поэтому равномерное движение возможно лишь в трубах постоянного сечения S, так как в противном случае будет изменяться средняя скорость в соответствии с уравнением:
• v = Q/S = const.

Равномерное движение имеет место в прямых трубах или в трубах с очень большим радиусом кривизны R (прямолинейное движение), так как в противном случае средняя скорость может изменяться по направлению.

Кроме того, условие неизменности характера скоростей жидкости по живому сечению можно записать в виде α = const, где α – коэффициент Кориолиса. Последнее условие может быть соблюдено лишь при достаточном удалении рассматриваемого участка потока от входа в трубу.

1. Если выделить на участке трубы с равномерно текущей жидкостью два произвольных сечения 1 и 2, то потери напора при перемещении жидкости между этими сечениями можно описать при помощи уравнения Бернулли:
2. z1 + p1/γ = z2 + p2/γ +hтр,
3. где: z1 и z2 – перепад высот между центрами соответствующих сечений; p1 и p2 – давление жидкости в соответствующих сечениях; γ – удельная плотность жидкости, γ = gρ;
4. hтр – величина потерянной энергии (потери на трение).
5. Из этой формулы выразим величину потерянной энергии hтр:
6. hтр = (z1 + p1/γ) — (z2 + p2/γ).

Это выражение называют уравнением равномерного движения жидкости в трубопроводе. Если труба расположена горизонтально, т. е. перепад высот между ее сечениями отсутствует, то уравнение примет упрощенный вид:

hтр = p1/γ — p2/γ = (p1 – p2)/γ.

***

Формула Дарси-Вейсбаха для равномерного движения жидкости в трубах

• При равномерном движении жидкости в трубах потери напора на трение по длине hл определяют по формуле Дарси-Вейсбаха, которая справедлива для круглых труб, как при турбулентном, так и при ламинарном режиме. Эта формула устанавливает зависимость между потерями напора hл, диаметром трубы d и средней скоростью потока жидкости v:
• hл = λv2/2gd,
• где: λ – коэффициент гидравлического трения (величина безразмерная);
• g – ускорение свободного падения.
• Для труб произвольного сечения в формуле Дарси-Вейсбаха используют понятие приведенного или эквивалентного диаметра сечения трубы по отношению к круглому сечению.
• В некоторых случаях используют также формулу
• hл = v2l/C2R,
• где: v – средняя скорость потока в трубе или канале; l – длина участка трубы или канала; R – гидравлический радиус потока жидкости;

С – коэффициент Шези, связанный с коэффициентом гидравлического трения λ зависимостью: С = √(8g/λ) или λ = 8g/С2. Размерность коэффициента Шези – м1/2/с.

Для определения коэффициента гидравлического трения при различных режимах и условиях движения жидкости применяют различные способы и эмпирические зависимости, в частности, график И. И.

Никурадзе, формулы П. Блазиуса, Ф. А. Шевелева (для гладких труб) и Б. Л. Шифринсона (для шероховатых труб).

Все эти способы и зависимости опираются на критерий Рейнольдса Re и учитывают состояние поверхности труб.

***

Потери напора из-за местных сопротивлений

Как уже указывалось выше, местные потери напора обусловлены преодолением местных сопротивлений, создаваемых фасонными частями, арматурой и прочим оборудованием трубопроводных сетей, а также изменением направления потока жидкости (изгибы труб, колена и т. п.). Местные сопротивления вызывают изменение величины или направления скорости движения жидкости на отдельных участках трубопровода, что связано с появлением дополнительных потерь напора.

1. Движение в трубопроводе при наличии местных сопротивлений является неравномерным.
2. Потери напора в местных сопротивлениях hм (местные потери напора) вычисляют по формуле Вейсбаха:
3. hм = ξv2/2g,
4. где: v – средняя скорость в сечении, расположенном ниже по течению за местным сопротивлением; ξ – безразмерный коэффициент местного сопротивления, определяемый для каждого вида местного сопротивления по справочным таблицам или установленным зависимостям.
5. Потери напора при внезапном расширении трубопровода находят по формуле Борда:

hвн.р. = (v1 – v2)22g = ξвн.р.1v12/2g = ξвн.р.2v22/2g,

где v1 и v2 – средние скорости течения до и после расширения.

При внезапном сужении трубопровода коэффициент местного сопротивления определяется по формуле:

hвн.с. = (1/ε — 1)2,

где ε — коэффициент сжатия струи, определяемый, как отношение площади сечения сжатой струи в узком трубопроводе к площади сечения узкой трубы. Этот коэффициент зависит от степени сжатия потока n = S2/S1 и может быть найден по формуле А. Д. Альтшуля:    ε = 0,57 + 0,043/(1,1 — n). Значение коэффициента ε при расчетах трубопроводов берут из справочных таблиц.

• При резком повороте трубы круглого поперечного сечения на угол α коэффициент сопротивления можно найти по формуле:
• ξα = ξ90˚(1 – cos α),
• где: ξ90˚ — значение коэффициента сопротивления для угла 90˚, которое для точных расчетов принимается по справочным таблицам, а для приближенных расчетов принимается равным ξ90˚ = 1.

Аналогичными методами осуществляют подбор или расчет коэффициентов сопротивления для других видов местных сопротивлений – резкое или постепенное сужение (расширение) трубопровода, повороты, входы и выходы из трубы, диафрагмы, запорные устройства, сварочные швы и т. п.

Приведенные выше формулы применимы для турбулентного режима движения жидкостей с большими числами Рейнольдса, когда влияние вязкости жидкости незначительно.

При движении жидкости с малыми числами Рейнольдса (ламинарный режим) величина местных сопротивлений мало зависит от геометрических характеристик сопротивления и скорости потока, на их величину большее влияние оказывает величина числа Рейнольдса.

В таких случаях для расчета коэффициентов местных сопротивлений применима формула А. Д. Альтшуля:

1. ξ = А/Re + ξэкв,
2. где: А – нестесненное сечение трубопровода;
3. ξэкв – значения коэффициента местного сопротивления в квадратичной области;
4. Значения параметра А и некоторых местных сопротивлений приводятся в справочных таблицах и используются при практических расчетах трубопроводов, предназначенных для движения жидкостей в ламинарном режиме.
5. ***
6. Трубопроводы и их гидравлический расчет
7. k-a-t.ru

Re — число Рейнольдса.

Трубопроводы для транспортировки различных жидкостей являются неотъемлемой частью агрегатов и установок, в которых осуществляются рабочие процессы, относящиеся к различным областям применения.

При выборе труб и конфигурации трубопровода большое значение имеет стоимость как самих труб, так и трубопроводной арматуры. Конечная стоимость перекачки среды по трубопроводу во многом определяется размерами труб (диаметр и длина).

Расчет этих величин осуществляется с помощью специально разработанных формул, специфичных для определенных видов эксплуатации.

Труба – это полый цилиндр из металла, дерева или другого материала, применяемый для транспортировки жидких, газообразных и сыпучих сред. В качестве перемещаемой среды может выступать вода, природный газ, пар, нефтепродукты и т.д. Трубы используются повсеместно, начиная с различных отраслей промышленности и заканчивая бытовым применением.

Для изготовления труб могут использоваться самые разные материалы, такие как сталь, чугун, медь, цемент, пластик, такой как АБС-пластик, поливинилхлорид, хлорированный поливинилхлорид, полибутелен, полиэтилен и пр.

Основными размерными показателями трубы являются ее диаметр (наружный, внутренний и т.д.) и толщина стенки, которые измеряются в миллиметрах или дюймах.

Также используется такая величина как условный диаметр или условный проход – номинальная величина внутреннего диаметра трубы, также измеряемая в миллиметрах (обозначается Ду) или дюймах (обозначается DN).

Величины условных диаметров стандартизированы и являются основным критерием при подборе труб и соединительной арматуры.

Соответствие значений условного прохода в мм и дюймах:

Трубе с круглым поперечным сечением отдают предпочтение перед другими геометрическими сечениями по ряду причин:

• Круг обладает минимальным соотношением периметра к площади, а применимо к трубе это означает, что при равной пропускной способности расход материала у труб круглой формы будет минимальным в сравнении с трубами другой формы. Отсюда же следует и минимально возможные затраты на изоляцию и защитное покрытие;
• Круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды с гидродинамической точки зрения. Также за счет минимально возможной внутренней площади трубы на единицу ее длины достигается минимизация трения между перемещаемой средой и трубой.
• Круглая форма наиболее устойчива к воздействию внутренних и внешних давлений;
• Процесс изготовления труб круглой формы достаточно прост и легкоосуществим.

Трубы могут сильно отличаться по диаметру и конфигурации в зависимости от назначения и области применения. Так магистральные трубопроводы для перемещения воды или нефтепродуктов способны достигать почти полуметра в диаметре при достаточно простой конфигурации, а нагревательные змеевики, также представляющие собой трубу, при малом диаметре имеют сложную форму с множеством поворотов.

Невозможно представить какую-либо отрасль промышленности без сети трубопроводов. Расчет любой такой сети включает подбор материала труб, составление спецификации, где перечислены данные о толщине, размере труб, маршруте и т.д.

Сырье, промежуточный продукт и/или готовый продукт проходят производственные стадии, перемещаясь между различными аппаратами и установками, которые соединяются при помощи трубопроводов и фитингов.

Правильный расчет, подбор и монтаж системы трубопроводов необходим для надежного осуществления всего процесса, обеспечения безопасной перекачки сред, а также для герметизации системы и недопущения утечек перекачиваемого вещества в атмосферу.

Не существует единой формулы и правил, которые могли бы быть использованы для подбора трубопровода для любого возможного применения и рабочей среды.

В каждой отдельной области применения трубопроводов присутствует ряд факторов, требующих учета и способных оказать значительное влияние на предъявляемые к трубопроводу требования.

Так, например, при работе со шламом, трубопровод большого размера не только увеличит стоимость установки, но также создаст рабочие трудности.

Обычно трубы подбирают после оптимизации расходов на материал и эксплуатационных расходов. Чем больше диаметр трубопровода, то есть выше изначальное инвестирование, тем ниже будет перепад давления и соответственно меньше эксплуатационные расходы.

И наоборот, малые размеры трубопровода позволят уменьшить первичные затраты на сами трубы и трубную арматуру, но возрастание скорости повлечет за собой увеличение потерь, что приведет к необходимости затрачивать дополнительную энергию на перекачку среды.

Нормы по скорости, фиксированные для различных областей применения, базируются на оптимальных расчетных условиях. Размер трубопроводов рассчитывают, используя эти нормы с учетом областей применения.

Проектирование трубопроводов

При проектировании трубопроводов за основу берутся следующие основные конструктивные параметры:

• требуемая производительность;
• место входа и место выхода трубопровода;
• состав среды, включая вязкость и удельный вес;
• топографические условия маршрута трубопровода;
• максимально допустимое рабочее давление;
• гидравлический расчет;
• диаметр трубопровода, толщина стенок, предел текучести материала стенок при растяжении;
• количество насосных станций, расстояние между ними и потребляемая мощность.

Надежность трубопроводов

Надежность в конструировании трубопроводов обеспечивается соблюдением надлежащих норм проектирования.

Также обучение персонала является ключевым фактором обеспечения длительного срока службы трубопровода и его герметичности и надежности.

Постоянный или периодический контроль работы трубопровода может быть осуществлен системами контроля, учёта, управления, регулирования и автоматизации, персональными приборами контроля на производстве, предохранительными устройствами.

Дополнительное покрытие трубопровода

Коррозионно-стойкое покрытие наносят на наружную часть большинства труб для предотвращения разрушающего действия коррозии со стороны внешней среды.

В случае перекачивая коррозионных сред, защитное покрытие может быть нанесено и на внутреннюю поверхность труб.

Перед вводом в эксплуатацию все новые трубы, предназначенные для транспортировки опасных жидкостей, проходят проверку на дефекты и протечки.

Основные положения для расчета потока в трубопроводе

Характер течения среды в трубопроводе и при обтекании препятствий способен сильно отличаться от жидкости к жидкости. Одним из важных показателей является вязкость среды, характеризуемая таким параметром как коэффициент вязкости.

Ирландский инженер-физик Осборн Рейнольдс провел серию опытов в 1880г, по результатам которых ему удалось вывести безразмерную величину, характеризующую характер потока вязкой жидкости, названную критерием Рейнольдса и обозначаемую Re.

• Re = (v·L·ρ)/μ
• где: ρ — плотность жидкости; v — скорость потока; L — характерная длина элемента потока;
• μ – динамический коэффициент вязкости.

То есть критерий Рейнольдса характеризует отношение сил инерции к силам вязкого трения в потоке жидкости. Изменение значения этого критерия отображает изменение соотношения этих типов сил, что, в свою очередь, влияет на характер потока жидкости. В связи с этим принято выделять три режима потока в зависимости от значения критерия Рейнольдса. При Re