Формула местной скорости трубопровода

Диаметр трубопроводов, скорость течения и расход теплоносителя.

В системе водяного отопления особенно часто у многих встает вопрос: Как вычислить диаметр трубопровода, по которому будет бежать теплоноситель (вода).

Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.

Для того чтобы вычислить диаметр необходимо знать:

1. Расход теплоносителя (воды) в трубе. 2. Сопротивление движению теплоносителя (воды) в трубе определенной длины.

Вот необходимые формулы, которые нужно знать:

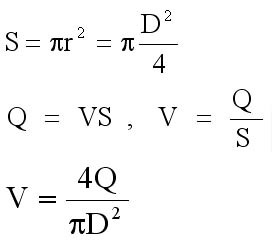
S-Площадь сечения м2 внутреннего просвета трубы π-3,14-константа — отношение длины окружности к ее диаметру. r-Радиус окружности, равный половине диаметра, м Q-расход воды м3/с D-Внутренний диаметр трубы, м V-скорость течения теплоносителя, м/с

Сопротивление движению теплоносителя.

Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя — является силой сопротивления.

Это сопротивление, называют — потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.

Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.

Извиняйте, но я привык указывать потерю напора в метрах. 10 метров водного столба создают 0,1 МПа.

• Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.
• Задача 1.

В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.

Решение: Необходимо воспользоваться вышеуказанными формулами:

1. Находим сечение 2. Находим расход

1. Дано:
2. S=3.14•0,0122/4=0,000113 м2
3. Q=0,000113•1=0,000113 м3/с = 0,4 м3/ч.
4. Ответ: 0,4 м3/ч.
5. Задача 2.

Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.

Конечно, в реальности насосы не выдают постоянный расход и не выдают бесконечно большой напор. Поэтому по условию задачи мы условно приняли, что насос качает строго 40 литров в минуту, а напор насоса бесконечно большой.

Ниже я поясню все нюансы подбора диаметра.

• Решение.
• Дано:
• Q=40л/мин=0,000666666 м3/с
• Из выше указанных формул получил такую формулу.

Ответ: 12мм

К сожалению, по такой формуле находить диаметр трубы не разумно и вот почему!

Каждый насос имеет вот такую расходно-сопротивляемую характеристику:

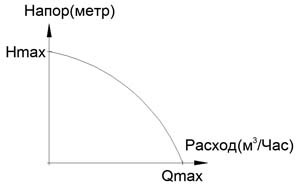
Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.

Чем длиннее труба, тем больше потеря напора. Чем меньше диаметр, тем больше потеря напора. Чем выше скорость теплоносителя в трубе, тем больше потеря напора. Углы, повороты, тройники, заужения и расширение трубы, тоже увеличивают потерю напора.

Такой характеристикой обладают на самом деле не насосы, а жидкости, которые подчиняются гидравлическим законам. Эти законы распространяются не только на насосы, но и на все трубы по которым течет жидкость.

Даже если вода будет истекать из наполненного бака, там тоже будет присутствовать такая вот расходно-сопротивляемая характеристика.

1. Более детально потеря напора по длине трубопровода рассматривается в этой статье:
2. Потеря напора по длине трубопровода.

3. А теперь рассмотрим задачу из реального примера.
4. Хочу сразу Вас уведомить, что для следующей задачи были использованы эти материалы:
5. Профессиональный расчет диаметра трубы для водоснабжения.
6. Задача 2:

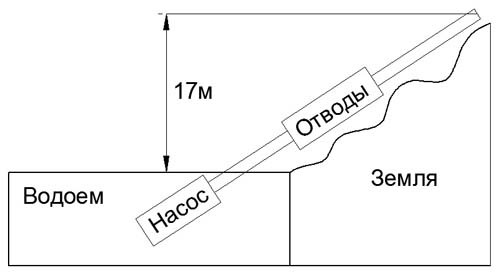
Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м3/ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.

Дано:

D=100 мм = 0,1м L=376м Геометрическая высота=17м Отводов 21 шт Напор насоса= 0,5 МПа (50 метров водного столба) Максимальный расход=90м3/ч Температура воды 16°С. Труба стальная железная

Найти максимальный расход = ?

Решение на видео:

• Купить программу
• Для решения необходимо знать график насосов: Зависимость расхода от напора.

Я выбрал визуально похожий график всех насосов, от реального может отличаться на 10-20%. Для более точного расчета необходим график насоса, который указан в паспорте насоса.

В нашем случае будет такой график:

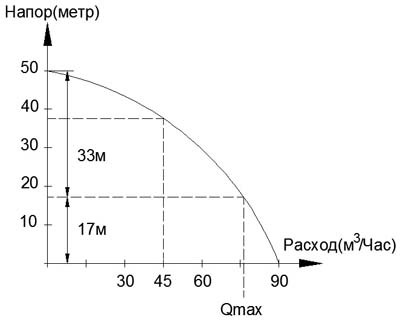
Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.

По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м3/час. (90-Qmax=14 м3/ч).

1. Не существует прямой формулы, которая дает прямой расчет нахождения расхода, а если и существует, то она имеет ступенчатый характер и некоторую логику, которая способна Вас запутать — окончательно.
2. Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
3. Поэтому решаем задачу ступенчато.
4. Поскольку мы имеем интервал расходов от 0 до 76 м3/час, то мне хочется проверить потерю напора при расходе равным: 45 м3/ч.
5. Находим скорость движения воды

• Q=45 м3/ч = 0,0125 м3/сек.
• V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
• Находим число рейнольдса

ν=1,16•10-6=0,00000116. Взято из таблици. Для воды при температуре 16°С.

Re=(V•D)/ν=(1,59•0,1)/0,00000116=137069

Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.

1. Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
2. У меня попадает на вторую область при условии
3. 10•D/Δэ < Re < 560•D/Δэ
4. 10•0,1/0,0001 < Re < 560•0,1/0,0001
5. 10 000 < Re < 560 000

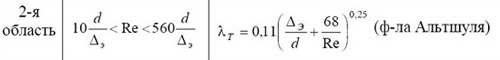
• λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/137069)0,25=0,0216
• Далее завершаем формулой:
• h=λ•(L•V2)/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
• Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:
• Теперь делаем оригинальный расчет при расходе равный 64м3/час
• Q=64 м3/ч = 0,018 м3/сек.
• V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
• Re=(V•D)/ν=(2,29•0,1)/0,00000116=197414
• λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/197414)0,25=0,021
• h=λ•(L•V2)/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
• Отмечаем на графике:
• Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).

Ответ: Максимальный расход равен 54 м3/ч. Но это мы решили без сопротивления на поворотах.

1. Для проверки проверим:
2. Q=54 м3/ч = 0,015 м3/сек.
3. V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
4. Re=(V•D)/ν=(1,91•0,1)/0,00000116=164655
5. λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/164655)0,25=0,0213
6. h=λ•(L•V2)/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
7. Итог: Мы попали на Нпот=14,89=15м.
8. А теперь посчитаем сопротивление на поворотах:
9. Формула по нахождению напора на местном гидравлическом сопротивление:
10. Подробней об этом в разделе: Местные гидравлические сопротивления

h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2

ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.

Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.

• Подробней об этом в разделе: Местные гидравлические сопротивления
• Возьмем ζ = 1.
• Скорость 1,91 м/с
• h=ζ•(V2)/2•9,81=(1•1,912)/( 2•9,81)=0,18 м.
• Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
• Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
• Давайте теперь решим целиком задачку с отводами.

При расходе 45 м3/час получили потерю напора по длине: 10,46 м. Смотри выше.

При этой скорости (2,29 м/с) находим сопротивление на поворотах:

h=ζ•(V2)/2•9,81=(1•2,292)/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.

1. Складываем потери напора: 10,46+5,67=16,13м.
2. Отмечаем на графике:
3. Решаем тоже самое только для расхода в 55 м3/ч
4. Q=55 м3/ч = 0,015 м3/сек.
5. V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
6. Re=(V*D)/ν=(1,91 •0,1)/0,00000116=164655
7. λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/164655)0,25=0,0213
8. h=λ•(L•V2)/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

h=ζ•(V2)/2•9,81=(1•1,912)/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.

• Складываем потери: 14,89+3,78=18,67 м
• Рисуем на графике:

Ответ: Максимальный расход=52 м3/час. Без отводов Qmax=54 м3/час.

1. Чтобы в ручную не считать всю математику я приготовил специальную программу:
2. Скачать калькулятор расчетов гидравлического сопротивления.

Теперь я думаю вам понятно как происходит сопротивление движению потока. Если не понятно, то я готов услышать ваши коментарии по данной статье. Пишите коментарии.

В итоге, на размер диаметра влияют:

1. Сопротивление, создаваемое трубой с поворотами 2. Необходимый расход 3. Влияние насоса его расходно-напорной характеристикой

Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.

Вычисляем диаметр трубы для отопления

Данная статья является частью системы: Конструктор водяного отопления

Основные формулы для гидравлического расчета трубопроводов

• Гидравлический расчет трубопроводов позволяет решать три основные задачи:
• 1) определять необходимый напор для пропуска известного расхода воды при заданном диаметре труб;
• 2) определять пропускную способность труб заданного диаметра при известных потерях напора;
• 3) определять сечение трубопроводов при заданных расходах воды и потерях напора.

Потери напора в трубопроводе слагаются из потерь на трение по длине и потерь на преодоление местных сопротивлений, т. е.

Потери напора по длине трубопроводов опреде­ляют по формуле Дарси—Вейсбаха:

1. где λ— коэффициент сопротивления трения по длине l; dp — расчетный внутренний диаметр труб, м; υ — средняя скорость движения жидкости, м/с; R — гидравлический радиус.
2. Если для круглой трубы определить скорость движения жид­кости
3. (1.105)
4. то потери напора по длине можно вычислить по формуле

где — удельное сопротивление, т. е. сопротивление 1 м трубопровода.

Сопротивление по всей длине / трубопровода составит Sl = Аl1 и тогда

Потери напора на единицу длины трубопровода называют гид­равлическим уклоном i, т. е.

Коэффициент сопротивления λ при движении воды в новых и бывших в эксплуатации трубопроводах из различных материалов определяют по зависимостям, полученным во ВНИИ ВОДГЕО д-ром техн. наук Ф. А. Шевелевым:

для новых стальных труб

для стальных чугунных труб, бывших в эксплуатации

При гидравлических расчетах водопроводных труб удельное сопротивление можно подсчитать по формуле, составленной с учетом увеличения коэффициента X вследствие возрастания шероховато­сти стенок труб во время их эксплуатации в результате коррозии или образования отложений:

Эта формула справедлива при скорости движения воды υ ≥1,2 м/с. При меньших скоростях в значения удельных сопротивле­ний вводится поправочный коэффициент Кn на неквадратичность зависимости потерь напора от средней скорости движения жидкости. Тогда формулы (1.106) и (1.107) приобретают такой вид:

(1.110)

Значения поправочного коэффициента Кn изменяютсяот 1 до1,4 при изменении скорости от 1,2до 0,2 м/с. Поправочныйкоэффи­ циент определяют по формуле

• Потери напора на преодоление местных сопротивлений определяют по формуле:
• (1.111)
• По аналогии с формулой (1.106) можно записать

При расчетах трубопроводов местные потери можно выразить ввиде потерь напора на трение по эквивалентной длине. При этом hм = hlэ , т. е. Σ ζQAмlQ2 = AtLэQ2 или Allэ = АмΣ ζ, откуда

(1.112)

Величину 1Э называют эквивалентной длиной трубопровода, соответствующей данному местному сопротивлению с коэффициен­том ζ.

Расход можно определить из уравнения (1.107): Q = . Для определения расхода и скорости жидкости, протекающей по трубопроводу, пользуются также (преимущественно для каналов и труб некруглого сечения) уравнением Шези: . Приме­нение уравнения Шези изложено в § 38.

1. При расчете трубопроводов используют не только удельное и общее сопротивление Аl, и Sl, но и другие гидравлические харак­теристики, например, проводимость трубопроводов:
2. (1.113)
3. — расходная характеристика:
4. (1.114)
5. Расходная характеристика и проводимость, соответствующие местным сопротивлениям, по аналогии будут представлены следую­щими соотношениями:
6. и

Расход жидкости, движущейся по трубопроводу, может быть оп­ределен через проводимость Рl т. е.

(1.115)

Для упрощения расчетов по приведенным формулам составлены таблицы значений удельных сопротивлений Аl с поправочным ко­эффициентом Кn (прил. 1). При гидравлическом расчете стальных труб стандартных диаметров можно использовать прил. 2.

• Диаметр трубопровода определяют в зависимости от расхода перекачиваемой жидкости и скорости ее движения по формуле
• где d —диаметр трубы, м; Q — расчетный расход воды, м3/с; υ— средняя скорость движения, м/с; для малых диаметров (до 400 мм) υпринимается в прц-делах 0,7—1 м/с, а для средних и больших диаметров — 1 — 1,5 м/с.

Следует иметь в виду, что с уменьшением диаметров трубо-провода'при одном и том же расходе увеличиваются скорость и по­тери напора, а с увеличением скорости и потерь напора возрастают эксплуатационные расходы. С увеличением же диаметра трубопро­вода скорость и потери напора уменьшаются. В связи с этим при

определении диаметра трубопровода необходимо учитывать требова­ния экономичности и технической целесообразности, иначе говоря, стремиться к определению экономически наивыгоднейшего диаметра, соответствующего минимуму его приведенной стоимости, включаю­щей затраты на строительство и на эксплуатацию трубопровода. Выбор экономичного диаметра трубопровода приобретает осо­бое значение при гидравлическом расчете внешних водопроводных сетей. Экономически наивыгоднейшие диаметры водопроводных труб определяют по расчетному расходу воды с учетом экономиче­ского фактора Э по формуле

Величина Э, зависящая главным образом от стоимости электро­энергии, труб и их укладки, изменяется от0,5 до 1 (для европейской части СССР Э = 0,75).

Для ускорения гидравлического расчета водопроводных труб пользуются таблицами, составленными Ф. А. Шевелевым (см. прил. 2).

Самостоятельный гидравлический расчет трубопровода

• Содержание: [Скрыть]

Постановка задачи

Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя.

Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.

• минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
• круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
• форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
• процесс изготовления труб круглой формы относительно простой и доступный.

Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.

Основными параметрами, характеризующими трубопровод являются:

• условный (номинальный) диаметр – DN;
• давление номинальное – PN;
• рабочее допустимое (избыточное) давление;
• материал трубопровода, линейное расширение, тепловое линейное расширение;
• физико-химические свойства рабочей среды;
• комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
• изоляционные материалы трубопровода.

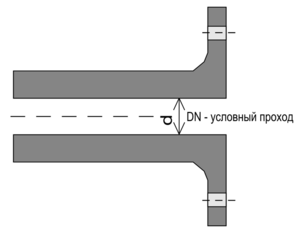Условный диаметр (проход) трубопровода (DN) – это условная  безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).

Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.

Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода.

Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.

Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.

Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.

Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.

Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.

Основные положения гидравлического расчета

Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.

Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний,  по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:

Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:

• ламинарный поток (Re

Скорость воды в трубопроводе: факторы и расчеты

Сооружая автономную водопроводную сеть для частного дома, необходимо задуматься о достаточно большом количестве параметров, которые сделают водопровод сетью, работающей долгое время и не требующей больших затрат на ее обслуживание. Один из важных факторов – скорость движения воды в трубопроводах водоснабжения.

Почему скорость должна быть определенного значения

Скорость воды в трубах учитывают при выборе материала и диаметра трубопровода

Если скорость недостаточная, на стенках труб будут осаждаться нерастворенные частицы, которые поступают с водой из скважины или колодца. Это приведет к заиливанию и уменьшению проходного сечения. В результате снизится напор и производительность всей системы в целом.

Если скорость воды в водопроводе большая, это приводит к увеличению давления перекачиваемой жидкости на стенки труб и их стыки. Велика вероятность, что в каком-то месте трубопровода со временем произойдет протечка.

Типовые значения скорости

Существуют рекомендованные значения скорости водяного потока в трубах водоснабжения, которые зависят от материала, из которого водопроводные трубы изготовлены, новые они или уже были в эксплуатации. Вот несколько зависимостей, которые помогут сделать правильный выбор.

Скорость в пластиковой трубе м/сек	Скорость в стальной трубе, м/сек
новая	старая
50	22	0,7	0,062
100	11	0,74	0,068
200	7,6	0,82	0,076

Скорость напрямую зависит и от диаметра труб. При этом любые жидкости, движущиеся по трубам, подчиняются законам физики. В водопроводе эти законы стремятся остановить движение воды. Сила, которая к этому прикладывается, называется силой сопротивления. Она ведет к потерям напора, а соответственно и к снижению скорости.

Обычно формулу скорости потока воды в трубопроводах, как таковую, не применяют нигде. Потому что нет смысла рассчитывать то, что уже доказано и находится в свободном доступе в таблицах. Ее принимают, как стандартную рекомендованную величину.

Сам параметр скорости потока воды в трубопроводах применяют для расчета нескольких характеристик водопроводной сети. К примеру, при расчете расхода воды или выбора диаметра труб.

Под водопроводом надо понимать сети питьевой воды, горячего водоснабжения и противопожарной системы.

Примеры расчетов

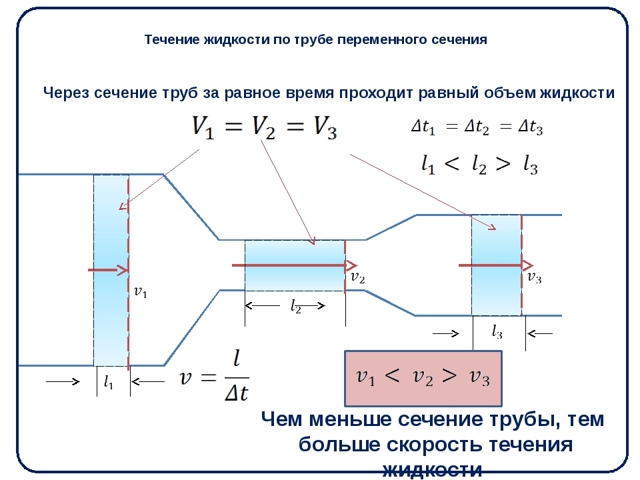Чаще с помощью скорости рассчитывают расход воды или диаметр труб. Для этого используют формулу:

W= V×S, где W – расход, V – скорость, S – площадь сечения выбранных труб.

По одной из таблиц выбирается скорость движения воды. Если это пожарный водопровод, в нем данный параметр должен быть в пределах 3 м/с. Достаточно большое значение, но для водопровода этого типа величина усредненная, бывает и больше.

К примеру, надо рассчитать сечение трубы. Для этого дополнительно нужно определиться, сколько воды будет расходоваться через спринклеры или дренчеры противопожарной системы. Это также табличная величина, зависящая от защищаемой площади здания или сооружения. Пусть это будет пожарная система в одну струю, в которой обычно расход составляет 3,5 л/сек или 0,0035 м³/час.

• Зная все требуемые параметры водопровода, можно рассчитать сечение труб, которые будут монтироваться в сеть:
• S=W/V=0,0035:3 = 0,0012 м².
• Зная сечение трубы, можно подсчитать ее диаметр. Формула площади такова: S=πD²/4, отсюда формула диаметра:

D=√4S/π=√(4×0,0012:3,14)=0,0038 м или 38 мм. Такого значения диаметра труб не существует, поэтому надо выбрать стандартное большее — 40 мм.

Это самый простой пример. В реальности большинство водопроводных систем – это сложные схемы, в которых присутствуют отводы, подсоединяемые участки, установленная запорная арматура и прочие препятствия, которые снижают быстроту движения воды в водопроводе.

При этом во многих сетях установлены насосные станции, которые формируют производительность и напор.

Нередко в систему устанавливаются насколько насосных агрегатов, которые работают попеременно: по два, по три, по одному, в разных последовательностях включения и отключения.

В таких случаях расчет проводят ступенчато, для каждого участка по отдельности. При этом обязательно учитываются дополнительные коэффициенты, которые нивелируют полученные значения, а также потери напора на фитингах и в местах установки запорной арматуры.

Скорость потока

Скорость воды в трубе имеет два значения: у стенок она равна нулю, у оси — максимальный параметр. Чем дальше от оси, тем слабее движется вода.

Если рассматривать цилиндр, по которому движется жидкость, как воображаемую модель, можно сказать, что на воду внутри трубы не будут действовать никакие силы. Но в реальности все не так. Первая сила, которая действует на водяной поток, — сила трения о внутренние стенки трубопровода. Она уменьшается с отдалением от стенок.

Вторая сила – нагнетающая, действующая от насоса в направлении движении потока. Если этот параметр всегда неизменный, течение жидкости внутри трубы происходит ламинарно. Скорость остается неизменной, у стенок она равна нулю. Это идеальная ситуация.

На практике так случается редко. Факторов для этого много, к примеру, включение и отключение насоса, засорение фильтра и так далее. В таком случае у стенок трубопроводов скорость изменяется резко: то больше, то меньше с иногда огромной разницей. В остальной части эта характеристика изменяется меньше.

Многие интернет-порталы предлагают калькуляторы, с помощью которых можно рассчитать скорость потока жидкости, проходящей через цилиндр. Для этого потребуется всего лишь два параметра:

• внутренний диаметр трубы в мм;
• производительность водопровода, а точнее, объем жидкости, проходящей через трубу за определенный промежуток времени (м³/час).

Но в таких калькуляторах не учитывается материал, из которого трубы изготовлены, а также наличие или отсутствие фитингов, дополнительных контуров и запорной арматуры. Эти расчетные сервисы можно взять за основу, но точного значения от них ждать не стоит.

Решая вопрос, связанный со скоростью перемещения водного потока внутри водопроводной сети, необходимо четко определиться со сложностью системы, производительностью насосных станций и видами используемых труб. Проще всего – подобрать это значение по таблице, в которой показатели давно рассчитаны и гарантированно достоверны.

Формула расчета скорости потока жидкости в трубе

Диаметр трубопроводов, скорость течения и расход теплоносителя.

Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.

Для того чтобы вычислить диаметр необходимо знать:

1. Расход теплоносителя (воды) в трубе. 2. Сопротивление движению теплоносителя (воды) в трубе определенной длины.

Вот необходимые формулы, которые нужно знать:

S-Площадь сечения м 2 внутреннего просвета трубы π-3,14-константа – отношение длины окружности к ее диаметру. r-Радиус окружности, равный половине диаметра, м Q-расход воды м 3 /с D-Внутренний диаметр трубы, м V-скорость течения теплоносителя, м/с

Сопротивление движению теплоносителя.

Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.

Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.

Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.

Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.

В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.

Решение: Необходимо воспользоваться вышеуказанными формулами:

1. Находим сечение 2. Находим расход

S=3.14•0,012 2 /4=0,000113 м 2

Q=0,000113•1=0,000113 м 3 /с = 0,4 м 3 /ч.

Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.

Q=40л/мин=0,000666666 м 3 /с

Из выше указанных формул получил такую формулу.

Каждый насос имеет вот такую расходно-сопротивляемую характеристику:

Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.

Чем длиннее труба, тем больше потеря напора. Чем меньше диаметр, тем больше потеря напора. Чем выше скорость теплоносителя в трубе, тем больше потеря напора. Углы, повороты, тройники, заужения и расширение трубы, тоже увеличивают потерю напора.

Более детально потеря напора по длине трубопровода рассматривается в этой статье:

А теперь рассмотрим задачу из реального примера.

Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м.

То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С.

Найти максимально возможный расход в конце трубы.

Читайте так же:  Утепление чердака каменной ватой

D=100 мм = 0,1м L=376м Геометрическая высота=17м Отводов 21 шт Напор насоса= 0,5 МПа (50 метров водного столба) Максимальный расход=90м 3 /ч Температура воды 16°С. Труба стальная железная

• Найти максимальный расход = ?
• Решение на видео:
• Для решения необходимо знать график насосов: Зависимость расхода от напора.

В нашем случае будет такой график:

Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.

По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).

1. Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
2. Поэтому решаем задачу ступенчато.
3. Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.
4. Находим скорость движения воды

• Q=45 м 3 /ч = 0,0125 м 3 /сек.
• V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
• Находим число рейнольдса

ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.

Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.

1. Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
2. У меня попадает на вторую область при условии
3. 10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216
4. Далее завершаем формулой:
5. h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
6. Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:

• Теперь делаем оригинальный расчет при расходе равный 64м 3 /час
• Q=64 м 3 /ч = 0,018 м 3 /сек.
• V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
• λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021
• h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
• Отмечаем на графике:
• Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).

Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.

1. Для проверки проверим:
2. Q=54 м 3 /ч = 0,015 м 3 /сек.
3. V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
4. λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
5. h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
6. Итог: Мы попали на Нпот=14,89=15м.
7. А теперь посчитаем сопротивление на поворотах:
8. Формула по нахождению напора на местном гидравлическом сопротивление:

h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2

Читайте так же:  Механическая очистка канализационных труб

ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.

Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.

• Скорость 1,91 м/с
• h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.
• Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
• Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
• Давайте теперь решим целиком задачку с отводами.

При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.

При этой скорости (2,29 м/с) находим сопротивление на поворотах:

h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.

1. Складываем потери напора: 10,46+5,67=16,13м.
2. Отмечаем на графике:
3. Решаем тоже самое только для расхода в 55 м 3 /ч
4. Q=55 м 3 /ч = 0,015 м 3 /сек.
5. V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
6. λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
7. h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.

h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.

• Складываем потери: 14,89+3,78=18,67 м
• Рисуем на графике:

Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.

В итоге, на размер диаметра влияют:

1. Сопротивление, создаваемое трубой с поворотами 2. Необходимый расход 3. Влияние насоса его расходно-напорной характеристикой

Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.

Данная статья является частью системы: Конструктор водяного отопления

Для правильного расчета должно быть известно назначение трубопровода: всасывающая магистраль, напорная или сливная.

Справочник по допустимой скорости жидкости в пределах этих типов магистралей приведен ниже. Расчетная скорость жидкости (м/с) должна находится в пределах этих диапазонов.

Чтобы вычислить скорость жидкости v (м/с), Вы должны ввести следующие данные:

1. Диаметр d (мм) – внутренний диаметр трубы. 2. Подача насоса Q (л/мин)

Читайте так же:  Как приготовить битумную мастику своими руками

Чтобы правильно подобрать трубу для всасывающей, напорной или сливной магистралей: 1. Выберите в таблице оптимальную скорость для соответствующей магистрали (v), м/сек 2. Введите подачу насоса Q (л/мин)

Нажмите «вычислить d»

Таблица рекомендуемой скорости потока рабочей жидкости в гидроприводе:

Наиболее экономичной скоростью воды в трубопроводе является скорость от 1-3 м/с. На крупных системах большая скорость, на малых системах меньшая. Принимаем среднюю скорость движения воды равной 1 м/с. Задаваясь скоростью равной 1 м/с, определяем диаметр трубопровода по формуле. В данном случае диаметр трубопровода по участкам расчетный.

1. , (2)
2. –число ПИ, соответствующее 3,14;
3. V – средняя скорость движения воды равная 1 м/с.

Единицу измерения расчетного диаметра переводим из м в мм. Используя таблицу 2, округляем полученные результаты диаметров до стандартных предпочтительно в большую сторону.

• Удельные сопротивления Акв (с 2 /м 6 ) труб из различных материалов в зависимости от условного прохода d
• Стальные электросварные ГОСТ 10704-76
• Чугунные ГОСТ 9583-75
• Полиэтиленовые типа Г ГОСТ 1899-73

5.4 Определение скорости движения воды в трубопроводе

1. По известным значениям расхода Qi и диаметра di определяется средняя скорость потока на каждом участке по формуле
2. , (3)
3. где Vi – скорость потока на каждом участке (м/c);
4. –число Пи (отношение длины окружности к радиусу), соответствующее 3,14;
5. Максимально допустимые скорости в магистральных трубопроводах не должны превышать 6 м/с, в распределительной сети 2-3 м/с.

5.5 Расчет потерь напора по участкам сети по преобразованной формуле д. Бернулли

Для водопроводных систем характерен сравнительно узкий интервал применяемых средних скоростей потоков (0,6…3,0 м/с). Поэтому в уравнении Д.

Бернулли можно пренебречь удельной кинетической энергией в сечении потока (она не превышает 0,46 м), а для ускорения расчета потерь напора на участках трубопровода использовать упрощенную зависимость, полученную путем преобразования формулы Дарси–Вейсбаха:

• , (4)
• где h – потери напора (м);
• kм – коэффициент, учитывающий влияние местных сопротивлений, которые составляют от 5 – 10% от сопротивления по длине [kм=1,05–1,1];
• Акв – удельное сопротивление трубы в квадратичной области, с 2 /м 6 ;
• – поправочный коэффициент, учитывающий неквадратичность области сопротивления;
• L – расчетная длина участка трубопровода, м;
• Qр – расчетный расход на участке трубопровода, м³/с.
• Соответствующие величины Акв и , которые представляются в уравнении (4) для вычисления потерь напора находятся по таблицам 2 и 3.
• Поправочный коэффициентна степень турбулентности потока в зависимости от скоростиV движения воды