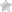Тема этой статьи – жидкость в трубе. Нам предстоит знакомство с физическими законами и формулами, описывающими ее движение, скорость и объем. Мы постараемся не лезть в дебри сложных расчетов: наша задача – описать те закономерности, которые будут понятны и доступны для вычисления человеку, далекому от гидродинамики.
Итак, приступим.
Нам предстоит знакомство с гидродинамикой, пусть и несколько поверхностное.
Размеры
Диаметр
В случае водопроводных и газовых труб мы имеем дело с не вполне обычной системой измерений. Для соответствующих трубопроводов в качестве основного параметра используется несколько непривычное понятие условного прохода, или условного диаметра (ДУ). Он измеряется как в дюймах, так и в миллиметрах; одна и та же ВГП труба может продаваться как 1 1/4 дюйма или ДУ32 мм.
Справка: в качестве меры длины в этом случае используется британский дюйм, равный 2,54 сантиметра. При пересчете дюймов в миллиметры следует учитывать предусмотренный ГОСТ шаг условных диаметров; так, в приведенном выше случае простой пересчет 1 1/4 дюйма в миллиметры даст не 32, а 1,25х2,54=31,75 мм.
Приведем предусмотренные ГОСТ 3262-75 размеры водогазопроводных труб.
| Условный проход (ДУ), мм | Фактический наружный диаметр, мм |
| 15 | 21,3 |
| 20 | 26,8 |
| 25 | 33,5 |
| 32 | 42,3 |
| 40 | 48,0 |
| 50 | 60,0 |
| 65 | 75,5 |
| 80 | 88,5 |
| 90 | 101,3 |
| 100 | 114,0 |
| 125 | 140,0 |
| 150 | 165,0 |
Поскольку толщина стенок варьируется в пределах одного типоразмера (трубы производятся легкими, обыкновенными и усиленными), можно сказать, что ДУ в общем случае близок к внутреннему диаметру, но, как правило, не равен ему.
Условный проход близок к внутреннему диаметру трубы.
Сечение
При строительстве водопроводов используются, за редким исключением, трубы круглого сечения.
Тому есть две весьма веских причины.
- У круглой трубы минимальная площадь стенок при максимальной площади сечения. Стало быть, цена погонного метра трубопровода при фиксированной толщине стенки будет минимальной – просто из-за меньшего расхода материала.
- Круглое сечение обеспечивает максимальную прочность на разрыв. Дело в том, что сила, с которой внутренняя среда с избыточным давлением давит на стенки, прямо пропорциональна их площади; а площадь, как мы уже выяснили, минимальна именно у круглой трубы.
Магистрали высокого давления всегда имеют круглое сечение.
Площадь внутреннего сечения вычисляется по формуле S=Pi*R^2, где S – искомое значение площади, Pi – число “пи”, приблизительно равное 3,14159265, а R – радиус (половина внутреннего диаметра). Скажем, у трубы с внутренним диаметром 200 мм сечение будет равно 3,14159265х(0,1^2)=0,031 м2.
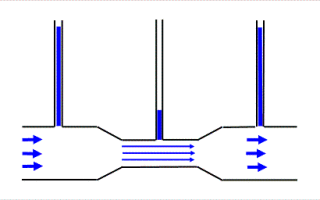
Поскольку течение жидкости в круглой трубе не всегда связано с заполнением всего ее объема, при расчетах нередко используется понятие “живого сечения”. Так называют площадь сечения потока. Скажем, при заполнении трубы ровно наполовину она будет равна (Pi*R^2)/2 (в приведенном выше примере – 0,031/2=0,00155 м2).
Живое сечение для напорной, самотечной канализации и для лотка.
Объем
Давайте выясним, чему равен объем жидкости в трубе. С точки зрения геометрии любая труба представляет собой цилиндр. Его объем рассчитывается как произведение площади сечения и длины.
Так, при площади сечения 0,031 м2 объем жидкости в полностью заполненном трубопроводе длиной 8 метров будет равен 0,031х8=0,248 м3.
При частично заполненной трубе для расчета используется среднее живое сечение. При постоянном уклоне и расходе движение жидкости по трубам будет равномерным; соответственно, живое сечение будет одинаковым на всех участках безнапорного трубопровода.
Расход
Разберемся, как выглядит расчет расхода жидкости через трубу. Задача имеет большую практическую ценность: она непосредственно связана с расчетами водопроводов при известном количестве сантехнических приборов.
Должны огорчить вас: простой и универсальной методики расчета не существует. Почему?
Просто потому, что при выполнении полного гидродинамического расчета своими руками нужно учитывать огромный ряд факторов:
- Коэффициент трения внутренней поверхности трубы. Очевидно, что шероховатая, покрытая отложениями сталь будет оказывать движению воды куда большее сопротивление, чем гладкий полипропилен.
Снимок позволяет оценить зарастание стальной трубы.
- Длина трубопровода. Чем большее расстояние предстоит пройти жидкости, тем большим будет падение напора из-за торможения потока о стенки, тем сильнее уменьшится расход.
- Диаметр трубопровода влияет на течение вязкой жидкости по трубам куда более сложным образом, чем это может показаться. Чем меньше сечение, тем большее сопротивление труба оказывает потоку. Причина – в том, что с уменьшением диаметра изменяется соотношение ее внутреннего объема и площади стенок.
Обратите внимание! В толстом трубопроводе ближняя к стенкам часть потока выполняет роль своеобразной смазки для его внутренней части. В тонком же толщина слоя этой смазки оказывается недостаточной.
- Наконец, каждый поворот трубопровода, переход диаметра, каждый элемент запорной арматуры тоже влияет на расход жидкости в нем, тормозя поток.
Повороты и элементы запорной арматуры вызывают падение напора.
Нужно понимать, что все перечисленные факторы влияют на результат вовсе не на единицы процентов: скажем, для новой стальной трубы с полированной внутренней поверхностью и для заросшей отложениями (даже без учета падения просвета) гидродинамическое сопротивление отличается более чем в 200 раз.
Для профессионалов все необходимые для гидравлического расчета трубопровода с учетом его полной конфигурации, материала и возраста данные приводятся в таблицах Ф.А. Шевелева. На основе этих таблиц создано много онлайн-калькуляторов, позволяющих выполнить расчет с той или иной степенью достоверности.
Есть, однако, одна лазейка, позволяющая существенно упростить самостоятельные расчеты. При расходе жидкости через отверстие, пренебрежимо малое по сравнению с подводящей жидкость трубой (что, собственно, мы и наблюдаем при работе большинства сантехнических приборов), действует закон Торричелли.
Эванджелиста Торричелли, один из основоположников гидродинамики.
Согласно этому закону, в описанном случае действует формула V^2=2gH, где V – скорость потока в отверстии, g – ускорение свободного падения (9,78 м*с^2), а H – высота столба над отверстием или, что то же самое, напор перед ним.
Справка: 1 атмосфера (1 кгс/см2) соответствует напору водяного столба в 10 метров.
Как скорость потока в отверстии увязывается с расходом? В нашем случае инструкция по расчету проста: через отверстие с площадью сечения S пройдет объем жидкости, равный произведению S на скорость потока V.
Давайте в качестве примера рассчитаем расход воды через отверстие диаметром 2 сантиметра при напоре в 10 метров, соответствующем одной атмосфере избыточного давления.
- V^2=2 х 9,78*10 = 195,6
- V равно квадратному корню из 195,6. Результат (13,985706 м/с) для простоты расчетов округлим до 14 м/с.
- Площадь сечения отверстия с диаметром в два сантиметра согласно приведенной выше формуле равна 3,14159265*0,01^2=0,000314159265 м2.
- Расход, стало быть, будет равным 0,000314159265*14=0,00439822971 м3/с. Для удобства переведем его в литры: поскольку 1 кубометр равен 1000 литров, в сухом остатке будет результат в 4,4 литра в секунду.
Для полноты картины приведем некоторые справочные данные.
| Сантехнический прибор | Средний расход воды, л/с |
| Умывальник с водоразборным краном | 0,1 |
| Умывальник со смесителем | 0,12 |
| Мойка со смесителем | 0,12 |
| Ванна со смесителем | 0,25 |
| Биде со смесителем и аэратором | 0,08 |
| Сливной бачок унитаза | 0,1 |
| Посудомоечная машина (набор воды) | 0,3 |
| Автоматическая стиральная машина | 0,25 |
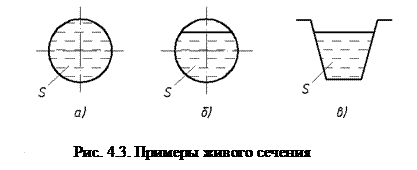
Заметьте: при последовательном подключении все задействованные приборы создают нагрузку на общую подводку.
Скорость потока
Как выглядит расчет скорости потока жидкости в трубе? В случае ее вытекания через отверстие небольшого диаметра действует приведенный выше закон Торричелли.
Однако в большинстве случаев скорость потока жидкости в трубе рассчитывается для трубопровода большой протяженности, гидравлическим сопротивлением которого нельзя пренебречь. Раз так – мы сталкиваемся с теми же проблемами: на скорость при постоянном перепаде на участке влияет слишком большое количество факторов.
Ситуация резко упрощается, если нам известен расход. Для несжимаемых жидкостей действует упрощенная формула уравнения непрерывности: Q=Av, где Q – расход воды в метрах в секунду, А – площадь полного или живого сечения, v – средняя скорость жидкости в трубе круглого сечения или любой другой формы.
Зная приведенные выше справочные данные расхода воды сантехприборами, нетрудно рассчитать скорость движения потока в водопроводной трубе известного диаметра.
В качестве примера давайте выясним, с какой скоростью будет двигаться вода в подводке ХВС с внутренним диаметром 15 мм (0,015 м) при одновременном наполнении сливного бачка, использовании посудомоечной машины и умывальника.
На фото – подводки водоснабжения в квартире. 15 мм – наиболее часто применяемый диаметр.
- Суммарный расход воды приборами, согласно приведенной выше таблице, составит 0,1 + 0,3 + 0,12 = 0,52 л/с, или 0,00052 м3/с.
- Площадь сечения трубы равна 3,14159265 х 0,0075 м^2 = 0,000176714865625 м2.
- Скорость потока в метрах в секунду равна 0,00052 / 0,000176714865625 = 2,96.
Для справки приведем некоторые значения скорости движения воды в трубопроводах различного назначения.
| Система | Диапазон скоростей, м/с |
| Самотечная система отопления | 0,2 – 0,5 |
| Система отопления с принудительной циркуляций, розлив | 0,5 – 3 |
| Система отопления с принудительной циркуляцией, подводки к отопительным приборам | 0,2 – 0,5 |
| Магистрали водоснабжения | 0,5 – 4 |
| Подводки водоснабжения | 0,5 – 1 |
| Циркуляция в системе ГВС | 0,2 – 0,5 |
| Безнапорная канализация (в том числе, ливневая канализация) | 0,35 – 1 |
Полезно: скорость потока до 1,5 м/с считается комфортной и не вызывающей ускорения абразивной эрозии стенок трубопровода. Приемлемо временное повышение скорости до 2,5 м/с.
Диаметр и давление
Еще один любопытный аспект поведения жидкости в трубе – взаимосвязь между скоростью потока и статическим давлением в нем. Она описывается законом Бернулли: статическое давление обратно пропорционально скорости потока.
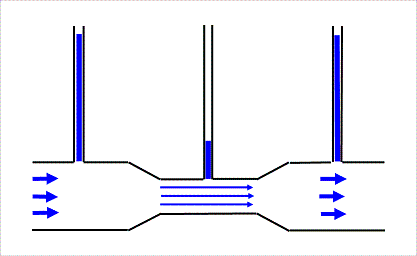
Наглядная демонстрация действия закона.
Практическое применение этого закона нашло воплощение во многих современных механизмах.
Приведем лишь пару примеров:
- Пневматический краскопульт работает именно за счет создаваемого в струе воздуха разрежения, которое буквально высасывает краситель из бачка и превращает его в переносимый на окрашиваемую поверхность аэрозоль.
- В элеваторном узле дома, подключенного к теплотрассе, разрежение в создаваемой соплом струе воды из подающего трубопровода вовлекает через подсос часть воды из обратки в повторный цикл циркуляции.
Схема работы элеватора.
Заключение
Надеемся, что читатель не нашел наш небольшой экскурс в основы физики, геометрии и гидродинамики слишком утомительным. Как обычно, дополнительную тематическую информацию можно обнаружить в видео в этой статье (см.также статью “Дымоходные трубы: монтаж и обслуживание”).
Успехов!
Самостоятельный гидравлический расчет трубопровода
- Содержание: [Скрыть]
Постановка задачи
Гидравлический расчёт при разработке проекта трубопровода направлен на определение диаметра трубы и падения напора потока носителя.
Данный вид расчёта проводится с учетом характеристик конструкционного материала, используемого при изготовлении магистрали, вида и количества элементов, составляющих систему трубопроводов(прямые участки, соединения, переходы, отводы и т. д.), производительности,физических и химических свойств рабочей среды.
- минимальное соотношением периметра к площади сечения, т.е. при равной способности, обеспечивать расход носителя, затраты на изолирующие и защитные материалы при изготовлении труб с сечением в виде круга, будут минимальными;
- круглое поперечное сечение наиболее выгодно для перемещения жидкой или газовой среды сточки зрения гидродинамики, достигается минимальное трение носителя о стенки трубы;
- форма сечения в виде круга максимально устойчива к воздействию внешних и внутренних напряжений;
- процесс изготовления труб круглой формы относительно простой и доступный.
Подбор труб по диаметру и материалу проводится на основании заданных конструктивных требований к конкретному технологическому процессу. В настоящее время элементы трубопровода стандартизированы и унифицированы по диаметру. Определяющим параметром при выборе диаметра трубы является допустимое рабочее давление, при котором будет эксплуатироваться данный трубопровод.
Основными параметрами, характеризующими трубопровод являются:
- условный (номинальный) диаметр – DN;
- давление номинальное – PN;
- рабочее допустимое (избыточное) давление;
- материал трубопровода, линейное расширение, тепловое линейное расширение;
- физико-химические свойства рабочей среды;
- комплектация трубопроводной системы (отводы, соединения, элементы компенсации расширения и т.д.);
- изоляционные материалы трубопровода.
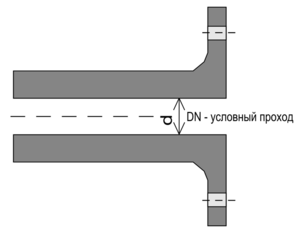Условный диаметр (проход) трубопровода (DN) – это условная безразмерная величина, характеризующая проходную способность трубы, приблизительно равная ее внутреннему диаметру. Данный параметр учитывается при осуществлении подгонки сопутствующих изделий трубопровода (трубы, отводы, фитинги и др.).
Условный диаметр может иметь значения от 3 до 4000 и обозначается: DN 80.
Условный проход по числовому определению примерно соответствует реальному диаметру определенных отрезков трубопровода.
Численно он выбран таким образом, что пропускная способность трубы повышается на 60-100% при переходе от предыдущего условного прохода к последующему.
Номинальный диаметр выбирается по значению внутреннего диаметра трубопровода. Это то значение, которое наиболее близко к реальному диаметру непосредственно трубы.
Давление номинальное (PN) – это безразмерная величина, характеризующая максимальное давление рабочего носителя в трубе заданного диаметра, при котором осуществима длительная эксплуатация трубопровода при температуре 20°C.
Значения номинального давления были установлены на основании продолжительной практики и опыта эксплуатации: от 1 до 6300.
Номинальное давление для трубопровода с заданными характеристиками определяется по ближайшему к реально создаваемому в нем давлению. При этом,вся трубопроводная арматура для данной магистрали должна соответствовать тому же давлению. Расчет толщины стенок трубы проводится с учетом значения номинального давления.
Основные положения гидравлического расчета
Рабочий носитель (жидкость, газ, пар), переносимый проектируемым трубопроводом, в силу своих особых физико-химических свойств определяет характер течения среды в данном трубопроводе. Одним из основных показателей характеризующих рабочий носитель, является динамическая вязкость, характеризуемая коэффициентом динамической вязкости – μ.
Инженер-физик Осборн Рейнольдс (Ирландия), занимавшийся изучением течения различных сред, в 1880 году провел серию испытаний, по результату которых было выведено понятие критерия Рейнолдса (Re) – безразмерной величины, описывающей характер потока жидкости в трубе. Расчет данного критерия проводится по формуле:
Критерий Рейнольдса (Re) дает понятие о соотношении сил инерции к силам вязкого трения в потоке жидкости. Значение критерия характеризует изменение соотношения указанных сил, что, в свою очередь, влияет на характер потока носителя в трубопроводе. Принято выделять следующие режимы потока жидкого носителя в трубе в зависимости от значения данного критерия:
- ламинарный поток (Re
Как определить расход воды по диаметру трубы и давлению?
Между давлением водного потока и трубным диаметром наблюдается прямая зависимость, описываемая законом Бернулли.
Согласно нему при возрастании давления воды скорость течения снижается, и наоборот.
При пропускании постоянного водного потока через трубы с различным сечением обнаруживается, что в узких частях давление меньше, чем в широких.
При переходе воды из широкой части в узкую, давление снижается, и наоборот.
В трубах с различным сечением за одинаковый промежуток времени протекает равный объем воды. Поэтому на широких участках она течет медленнее, чем по узким.
Таблица соотношения
Водорасход напрямую зависит от пропускной способности. Это такая величина, которая показывает максимальный объем, проходящий через систему за определенный временной промежуток и при определенном давлении.
Для труб с разным диаметром такая величина разнится. Подробная информация указана в таблице ниже:
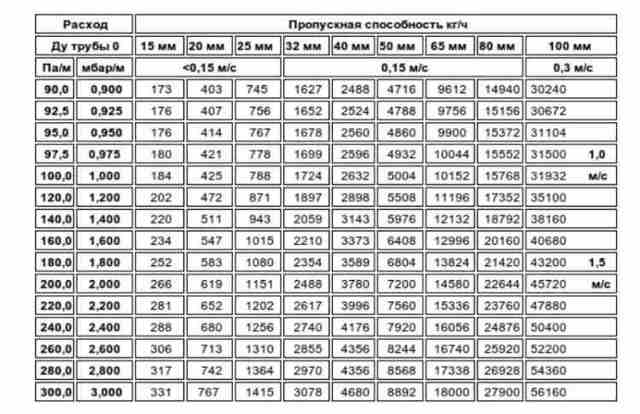
Когда нужно проводить вычисления?
Выполнять вычисления необходимо при выборе труб для водопровода. Диаметр должен быть подходящим, чтобы избежать чрезмерного водорасхода и обеспечить нормальный напор.
Такая необходимость появляется при проектировании дома и подведении к нему коммуникаций. При выборе трубы с оптимальным сечением для водопровода нужно обязательно выполнять ряд расчетов. Необходимо узнать максимальные объемы необходимой воды в доме за минуту.
Для этого нужно посмотреть паспортные данные стиральной и посудомоечной машин, узнать их расход. К полученным данным приплюсовать расход воды на кранах (через один прибор протекает примерно 5-6 литров за минуту времени).
Исходя из полученных результатов, нужно приобрести трубу с таким сечением, чтобы этого было достаточно для одновременной работы всех устройств и кранов.
Пошаговая инструкция, как рассчитать водорасход
Произвести подсчеты можно при помощи таблиц. Но полученные результаты будут неточными. Поэтому лучше проводить расчеты на месте, учитывая скорость потока, материал трубопроводных систем и прочие характеристики трубопровода.
Проще всего рассчитать объем расходуемой H2O по следующей формуле:
q=π*d2 /4*V, где:
- q – расход воды (л/с);
- V – скорость течения (м/с);
- d – диаметр (см).
Использовать эту формулу можно и для поиска других неизвестных. Если известен диаметр и расход воды, можно определить скорость потока. А если известны V и q, можно узнать диаметр.
В большинстве стояков напор водного потока равняется 1,5-2,5 атмосфер. А скорость потока обычно составляет 0,8-1,5 м/с. Может быть установлен дополнительный нагнетатель, который меняет параметры внутри системы. Все данные о нем должны быть указаны в техпаспорте.
Минимальное давление в системе должно составлять 1,5 атмосфер – этого достаточно для работы стиральной машины и посудомойки. Чем оно выше, тем быстрее вода движется по трубам, поэтому водорасход повышается.
Для получения более точных результатов применяется формула Дарси-Вейсбаха, которая учитывает возможные изменения напора воды, что приводит к повышению или снижению давления.
ΔP=λ*L/D*V2 /2q *ϸ, где:
- ΔP – потеря давления на сопротивлении движения потока;
- λ – показатель потерь на трение по всей длине;
- D – сечение трубы;
- V — скорость течения;
- L – длина трубопровода;
- g – константа = 9,8 м/с2;
- ϸ — вязкость потока.
Такую формулу обычно используют для выполнения сложных расчетов гидродинамики. В остальных случаях применяются упрощенные варианты.
Частный случай расчета водорасхода – через отверстие крана. Применяется формула:
q=S*V, где:
- Q – водорасход;
- S – площадь окружности (отверстия крана), определяется по формуле S= π*r2;
- V – скорость течения, если она неизвестна, определить ее можно, исходя из формулы V=2g*h, где g – константа, h – высота водного столба над отверстием крана.
Правила расчета
При выполнении вычислений необходимо учитывать следующие правила:
Следить за правильностью величин. Если одно значение исчисляется в м/с, то другое должно измеряться в л/с (не в кг/час). Иначе произведенные расчеты будут неверными.- Применять правильные значения констант.
- Учитывать данные нагнетателя системы, если он используется. Вся информация о его влиянии на параметры системы указывается в техническом паспорте.
- Промежуточные вычисления рекомендуется проводить с точными величинами, а конечный результат можно округлить (лучше в большую сторону).
Чтобы облегчить расчеты, можно воспользоваться калькуляторами в режиме онлайн, в которые достаточно только ввести все известные данные.
Заключение
Объем расходуемой воды напрямую зависит от трубного диаметра и давления внутри системы. Чем больше давление, тем быстрее будет протекать вода, что приведет к большому водорасходу. Чем меньше диаметр трубы, тем выше сопротивление воды и меньше скорость ее течения.
Если выбрать неподходящий d, водный напор в системе может быть снижен. Поэтому при установке водных коммуникаций нужно обязательно проводить расчеты. Иначе в будущем могут появиться проблемы с водорасходом.
Движение жидкости по трубам
Гидравлические сопротивления.
При течении жидкости по трубам ей приходится затрачивать энергию на преодоление сил внешнего и внутреннего трения. В прямых участках труб эти силы сопротивления действуют по всей длине потока и общая потеря энергии на их преодоление прямо пропорциональна длине трубы.
Такие сопротивления называются линейными.
Их величина (потеря давления) зависит от плотности и вязкости жидкости, а также от диаметра трубы (чем меньше диаметр, тем больше сопротивление), скорости течения (увеличение скорости увеличивает потери) и чистоты внутренней поверхности трубы (чем больше шероховатость стенок, тем больше сопротивление).
Кроме трения в прямых участках, в трубопроводах встречаются дополнительные сопротивления в виде поворотов потока, изменений сечения, кранов, ответвлений и т. п.
В этих случаях структура потока нарушается и его энергия затрачивается на перестроение, завихрения, удары. Такие сопротивления называют местными.
Линейные и местные сопротивления являются двумя разновидностями так называемых гидравлических сопротивлений, определение которых составляет основу расчета любых гидравлических систем.
Режимы течения жидкости.. В практике наблюдаются два характерных режима течения жидкостей: ламинарный и турбулентный.
При ламинарном режиме элементарные струйки потока текут параллельно, не перемешиваясь. Если в такой поток ввести струйку окрашенной жидкости, то она будет продолжать свое течение в виде тонкой нити среди потока неокрашенной жидкости, не размываясь. Такой режим течения возможен при очень малых скоростях потока.
С увеличением скорости выше определенного предела течение становится турбулентным, вихреобразным, при котором жидкость в пределах поперечного сечения трубопровода интенсивно перемешивается.
При постепенном увеличении скорости окрашенная струйка в потоке сначала начинает колебаться относительно своей оси, затем в ней появляются разрывы из-за перемешивания с другими струями и затем вследствие этого весь поток получает равномерную окраску.
Наличие того или иного режима течения зависит от величины отношения кинетической энергии потока 1 1
(■п-гпи2=ч-рУи2) к работе сил внут-реннего трения (/7 = р„5^/)-см. (2.9).
Это безразмерное отношение
^-pVv21 (р,5^/) можно упростить имея в виду, что Ды пропорционально V. Величины 1 и А/г также имеют одну и ту же размерность, и их можно сократить, а отношение объема V к поперечному сечению 5 является линейным размером й.
Тогда отношение кинетической энергии к работе сил внутреннего трения с точностью до постоянных множителей можно характеризовать безразмерным комплексом:
который называется числом (или критерием) Рейнольдса в честь английского физика Осборна Рейнольдса, в конце прошлого века экспериментально наблюдавшего наличие двух режимов течения.
Малые значения чисел Рейнольдса свидетельствуют о преобладании работы сил внутреннего трения в потоке жидкости и соответствуют ламинарному течению.
Большие значения Йе соответствуют преобладанию кинетической энергии и турбулентному режиму течения.
Граница начала перехода одного режима в другой — критическое число Рейнольдса — составляет 1?екр = 2300 для круглых труб (в качестве характерного размера принимается диаметр трубы).
В технике, в том числе и тепловозной, в гидравлических (в том числе воздушных и газовых) системах обычно имеет место турбулентное течение жидкостей. Ламинарный режим бывает лишь у вязких жидкостей (например, масло) при малых скоростях течения и в тонких каналах (плоские трубки радиатора).
где X («лямбда») — коэффициент линейного сопротивления, зависящий от числа Рейнольдса. Для ламинарного потока в круглой трубе Я, = 64/Ие (зависит от скорости), для турбулентных потоков величина к мало зависит от скорости и, главным образом, определяется шероховатостью стенок труб.
Местные потери напора также считаются пропорциональными квадрату скорости и определяются так:
где £ («дзета») — коэффициент местного сопротивления, зависящий от типа сопротивления (поворот, расширение и т. п.) и от его геометрических характеристик.
Коэффициенты местного сопротивления устанавливаются опытным путем, их значения приводятся в справочниках.
Понятие о расчете гидравлических систем. При расчете любой гидравлической системы решается обычно одна из двух задач: определение необходимого перепада давлений (напора) для пропуска данного расхода жидкости или определение расхода жидкости в системе при заданном перепаде давлений.
В любом случае должна быть определена полная потеря напора в системе АН, которая равна сумме сопротивлений всех участков системы, т. е. сумме линейных сопротивлений' всех прямых участков трубопроводов и местных сопротивлений других элементов системы:
Если во всех участках трубопровода средняя скорость течения одинакова, уравнение (2.33) упрощается:
Обычно в системе имеются участки, скорости течения в которых отличаются друг от друга. В этом случае удобно привести уравнение (2.33) к другой форме, учитывая что расход жидкости постоянен для всех элементов системы (без ответвлений). Подставив в условие (2.33) значения и = С}/5, получим
гидравлическая характеристика, или общий коэффициент сопротивления системы.
Необходимо иметь в виду, что расчет трубопроводов не является решением задачи с одним определенным ответом. Его результаты зависят от выбора величины диаметров участков трубопровода или скоростей в них.
Действительно, можно принять в расчете невысокие значения скоростей и получить небольшие потери напора. Но тогда при заданном расходе сечения трубопроводов (диаметры) должны быть большими, система будет громоздкой и тяжелой.
Приняв высокие скорости течения в трубах, мы уменьшим их поперечные размеры, но при этом существенно (пропорционально квадрату скорости) возрастут потери напора и затраты энергии на работу системы.
Поэтому при расчетах обычно задаются какими-то средними, «оптимальными», значениями скоростей течения жидкости. Для водяных систем оптимальная скорость имеет порядок примерно 1 м/с, для воздушных систем низкого давления — 8- 12 м/с.
Гидравлический удар представляет собой явление, происходящее в потоке жидкости при быстром изменении скорости его течения (например, при резком закрытии задвижки в трубопроводе или остановке насоса).
В этом случае кинетическая энергия потока мгновенно переходит в потенциальную энергию и давление потока перед задвижкой резко возрастает.
Область повышенного давления затем распространяется от задвижки в сторону еще не заторможенного полностью потока со скоростью, близкой к скорости звука а в этой среде.
Резкое повышение давления приводит если не к разрушению, то к упругой деформации элементов трубопровода, что уменьшает силу удара, но усиливает колебания давления жидкости в трубе.
Величина скачка давления при полной остановке потока жидкости, имевшего скорость v, определяется по формуле выдающегося русского ученого — профессора Н. Е. Жуковского, полученной им в 1898 г.
: Др = раа, где р — плотность жидкости.
С целью предотвращения ударных явлений в крупных гидравлических системах (например, водопроводных сетях) запорные устройства выполняют так, чтобы их закрытие происходило постепенно.
⇐ | Гидродинамика | | Тепловозы: Основы теории и конструкция | | Насосы и вентиляторы | ⇒
Формула расчета скорости потока жидкости в трубе
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.
Для того чтобы вычислить диаметр необходимо знать:
| 1. Расход теплоносителя (воды) в трубе. 2. Сопротивление движению теплоносителя (воды) в трубе определенной длины. |
Вот необходимые формулы, которые нужно знать:
| S-Площадь сечения м 2 внутреннего просвета трубы π-3,14-константа – отношение длины окружности к ее диаметру. r-Радиус окружности, равный половине диаметра, м Q-расход воды м 3 /с D-Внутренний диаметр трубы, м V-скорость течения теплоносителя, м/с |
Сопротивление движению теплоносителя.
Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.
Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.
Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.
Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.
В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.
Решение: Необходимо воспользоваться вышеуказанными формулами:
| 1. Находим сечение 2. Находим расход |
S=3.14•0,012 2 /4=0,000113 м 2
Q=0,000113•1=0,000113 м 3 /с = 0,4 м 3 /ч.
Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.
Q=40л/мин=0,000666666 м 3 /с
Из выше указанных формул получил такую формулу.
Каждый насос имеет вот такую расходно-сопротивляемую характеристику:
Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.
| Чем длиннее труба, тем больше потеря напора. Чем меньше диаметр, тем больше потеря напора. Чем выше скорость теплоносителя в трубе, тем больше потеря напора. Углы, повороты, тройники, заужения и расширение трубы, тоже увеличивают потерю напора. |
Более детально потеря напора по длине трубопровода рассматривается в этой статье:
А теперь рассмотрим задачу из реального примера.
Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м.
То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м 3 /ч. Температура воды 16°С.
Найти максимально возможный расход в конце трубы.
Читайте так же: Утепление чердака каменной ватой
| D=100 мм = 0,1м L=376м Геометрическая высота=17м Отводов 21 шт Напор насоса= 0,5 МПа (50 метров водного столба) Максимальный расход=90м 3 /ч Температура воды 16°С. Труба стальная железная |
- Найти максимальный расход = ?
- Решение на видео:
- Для решения необходимо знать график насосов: Зависимость расхода от напора.
В нашем случае будет такой график:
Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.
По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м 3 /час. (90-Qmax=14 м 3 /ч).
- Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
- Поэтому решаем задачу ступенчато.
- Поскольку мы имеем интервал расходов от 0 до 76 м 3 /час, то мне хочется проверить потерю напора при расходе равным: 45 м 3 /ч.
- Находим скорость движения воды
- Q=45 м 3 /ч = 0,0125 м 3 /сек.
- V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
- Находим число рейнольдса
ν=1,16•10 -6 =0,00000116. Взято из таблици. Для воды при температуре 16°С.
Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.
- Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
- У меня попадает на вторую область при условии
- 10•D/Δэ 0.25 =0,11•( 0,0001/0,1 + 68/137069) 0,25 =0,0216
- Далее завершаем формулой:
- h=λ•(L•V 2 )/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
- Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:
- Теперь делаем оригинальный расчет при расходе равный 64м 3 /час
- Q=64 м 3 /ч = 0,018 м 3 /сек.
- V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
- λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/197414) 0,25 =0,021
- h=λ•(L•V 2 )/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
- Отмечаем на графике:
- Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).
Ответ: Максимальный расход равен 54 м 3 /ч. Но это мы решили без сопротивления на поворотах.
- Для проверки проверим:
- Q=54 м 3 /ч = 0,015 м 3 /сек.
- V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
- λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
- h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
- Итог: Мы попали на Нпот=14,89=15м.
- А теперь посчитаем сопротивление на поворотах:
- Формула по нахождению напора на местном гидравлическом сопротивление:
| h-потеря напора здесь она измеряется в метрах. ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. V-скорость потока жидкости. Измеряется [Метр/секунда]. g-ускорение свободного падения равен 9,81 м/с2 |
Читайте так же: Механическая очистка канализационных труб
ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.
Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.
- Скорость 1,91 м/с
- h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м.
- Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
- Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
- Давайте теперь решим целиком задачку с отводами.
При расходе 45 м 3 /час получили потерю напора по длине: 10,46 м. Смотри выше.
При этой скорости (2,29 м/с) находим сопротивление на поворотах:
h=ζ•(V 2 )/2•9,81=(1•2,29 2 )/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.
- Складываем потери напора: 10,46+5,67=16,13м.
- Отмечаем на графике:
- Решаем тоже самое только для расхода в 55 м 3 /ч
- Q=55 м 3 /ч = 0,015 м 3 /сек.
- V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
- λ=0,11( Δэ/D + 68/Re ) 0.25 =0,11•( 0,0001/0,1 + 68/164655) 0,25 =0,0213
- h=λ•(L•V 2 )/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
h=ζ•(V 2 )/2•9,81=(1•1,91 2 )/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.
- Складываем потери: 14,89+3,78=18,67 м
- Рисуем на графике:
Ответ: Максимальный расход=52 м 3 /час. Без отводов Qmax=54 м 3 /час.
В итоге, на размер диаметра влияют:
| 1. Сопротивление, создаваемое трубой с поворотами 2. Необходимый расход 3. Влияние насоса его расходно-напорной характеристикой |
Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.
Данная статья является частью системы: Конструктор водяного отопления
Для правильного расчета должно быть известно назначение трубопровода: всасывающая магистраль, напорная или сливная.
Справочник по допустимой скорости жидкости в пределах этих типов магистралей приведен ниже. Расчетная скорость жидкости (м/с) должна находится в пределах этих диапазонов.
Чтобы вычислить скорость жидкости v (м/с), Вы должны ввести следующие данные:
1. Диаметр d (мм) – внутренний диаметр трубы. 2. Подача насоса Q (л/мин)
Читайте так же: Как приготовить битумную мастику своими руками
Чтобы правильно подобрать трубу для всасывающей, напорной или сливной магистралей: 1. Выберите в таблице оптимальную скорость для соответствующей магистрали (v), м/сек 2. Введите подачу насоса Q (л/мин)
Нажмите «вычислить d»
Таблица рекомендуемой скорости потока рабочей жидкости в гидроприводе:
Наиболее экономичной скоростью воды в трубопроводе является скорость от 1-3 м/с. На крупных системах большая скорость, на малых системах меньшая. Принимаем среднюю скорость движения воды равной 1 м/с. Задаваясь скоростью равной 1 м/с, определяем диаметр трубопровода по формуле. В данном случае диаметр трубопровода по участкам расчетный.
- , (2)
- –число ПИ, соответствующее 3,14;
- V – средняя скорость движения воды равная 1 м/с.
Единицу измерения расчетного диаметра переводим из м в мм. Используя таблицу 2, округляем полученные результаты диаметров до стандартных предпочтительно в большую сторону.
- Удельные сопротивления Акв (с 2 /м 6 ) труб из различных материалов в зависимости от условного прохода d
- Стальные электросварные ГОСТ 10704-76
- Чугунные ГОСТ 9583-75
- Полиэтиленовые типа Г ГОСТ 1899-73
5.4 Определение скорости движения воды в трубопроводе
- По известным значениям расхода Qi и диаметра di определяется средняя скорость потока на каждом участке по формуле
- , (3)
- где Vi – скорость потока на каждом участке (м/c);
- –число Пи (отношение длины окружности к радиусу), соответствующее 3,14;
- Максимально допустимые скорости в магистральных трубопроводах не должны превышать 6 м/с, в распределительной сети 2-3 м/с.
5.5 Расчет потерь напора по участкам сети по преобразованной формуле д. Бернулли
Для водопроводных систем характерен сравнительно узкий интервал применяемых средних скоростей потоков (0,6…3,0 м/с). Поэтому в уравнении Д.
Бернулли можно пренебречь удельной кинетической энергией в сечении потока (она не превышает 0,46 м), а для ускорения расчета потерь напора на участках трубопровода использовать упрощенную зависимость, полученную путем преобразования формулы Дарси–Вейсбаха:
- , (4)
- где h – потери напора (м);
- kм – коэффициент, учитывающий влияние местных сопротивлений, которые составляют от 5 – 10% от сопротивления по длине [kм=1,05–1,1];
- Акв – удельное сопротивление трубы в квадратичной области, с 2 /м 6 ;
- – поправочный коэффициент, учитывающий неквадратичность области сопротивления;
- L – расчетная длина участка трубопровода, м;
- Qр – расчетный расход на участке трубопровода, м³/с.
- Соответствующие величины Акв и , которые представляются в уравнении (4) для вычисления потерь напора находятся по таблицам 2 и 3.
- Поправочный коэффициентна степень турбулентности потока в зависимости от скоростиV движения воды
Загрузка...
